Fitting
from __future__ import annotations
import matplotlib.pyplot as plt
import numpy as np
from example_models import get_linear_chain_2v
from mxlpy import Simulator, fit, make_protocol, plot
Fitting¶
Almost every model at some point needs to be fitted to experimental data to be validated.
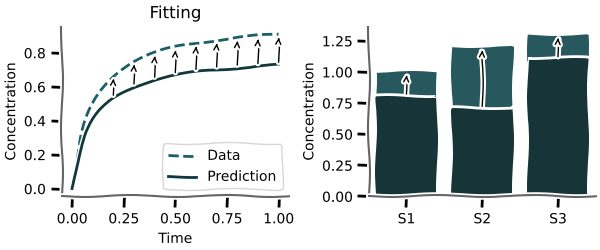
mxlpy offers highly customisable local and global routines for fitting either time series or steady-states.
The entire set of currently supported routines is
Single model, single data routines
steady_statetime_courseprotocol_time_course
Multiple model, single data routines
ensemble_steady_stateensemble_time_courseensemble_protocol_time_course
A carousel is a special case of an ensemble, where the general structure (e.g. stoichiometries) is the same, while the reactions kinetics can vary
carousel_steady_statecarousel_time_coursecarousel_protocol_time_course
Multiple model, multiple data
joint_steady_statejoint_time_coursejoint_protocol_time_course
Multiple model, multiple data, multiple methods
Here we also allow to run different methods (e.g. steady-state vs time courses) for each combination of model:data.
joint_mixed
Minimizers¶
- LocalScipyMinimizer, including common methods such as Nelder-Mead or L-BFGS-B
- GlobalScipyMinimizer, including common methods such as basin hopping or dual annealing
For this tutorial we are going to use the fit module to optimise our parameter values and the plot module to plot some results.
Let's get started!
Creating synthetic data¶
Normally, you would fit your model to experimental data.
Here, for the sake of simplicity, we will generate some synthetic data.
Checkout the basics tutorial if you need a refresher on building and simulating models.
# As a small trick, let's define a variable for the model function
# That way, we can re-use it all over the file and easily replace
# it with another model
model_fn = get_linear_chain_2v
res = (
Simulator(model_fn())
.update_parameters({"k1": 1.0, "k2": 2.0, "k3": 1.0})
.simulate_time_course(np.linspace(0, 10, 101))
.get_result()
.unwrap_or_err()
).get_combined()
fig, ax = plot.lines(res)
ax.set(xlabel="time / a.u.", ylabel="Conc. & Flux / a.u.")
plt.show()
Steady-states¶
For the steady-state fit we need two inputs:
- the steady state data, which we supply as a
pandas.Series - an initial parameter guess
The fitting routine will compare all data contained in that series to the model output.
Note that the data both contains concentrations and fluxes!
data = res.iloc[-1]
data.head()
x 0.500000 y 1.000045 v1 1.000000 v2 1.000000 v3 1.000045 Name: 10.0, dtype: float64
fit_result = fit.steady_state(
model_fn(),
p0={"k1": 1.038, "k2": 1.87, "k3": 1.093},
data=res.iloc[-1],
minimizer=fit.LocalScipyMinimizer(),
).unwrap_or_err()
fit_result.best_pars
{'k1': np.float64(1.0000151210679569),
'k2': np.float64(2.00003025575516),
'k3': np.float64(0.9999696973185731)}
If only some of the data is required, you can use a subset of it.
The fitting routine will only try to fit concentrations and fluxes contained in that series.
fit_result = fit.steady_state(
model_fn(),
p0={"k1": 1.038, "k2": 1.87, "k3": 1.093},
data=data.loc[["x", "y"]],
minimizer=fit.LocalScipyMinimizer(),
).unwrap_or_err()
fit_result.best_pars
/home/runner/work/MxlPy/MxlPy/.venv/lib/python3.12/site-packages/scipy/optimize/_numdiff.py:686: RuntimeWarning: invalid value encountered in subtract df = [f_eval - f0 for f_eval in f_evals]
{'k1': np.float64(1.038), 'k2': np.float64(1.87), 'k3': np.float64(1.093)}
By default, mxlpy will apply standard scaling to all fitting functions.
Specifically, it will calculate loss_fn(data - data.mean()) / data.std(), (pred - data.mean()) / data.std()).
To turn off this behaviour, set standard_scale=False in the fit functions
fit_result = fit.steady_state(
model_fn(),
p0={"k1": 1.038, "k2": 1.87, "k3": 1.093},
data=data.loc[["x", "y"]],
minimizer=fit.LocalScipyMinimizer(),
standard_scale=False, # opt-out of standard scaling
).unwrap_or_err()
fit_result.best_pars
{'k1': np.float64(0.9829446948021445),
'k2': np.float64(1.9658848491798002),
'k3': np.float64(0.9829008077692354)}
Time course¶
For the time course fit we need again need two inputs
- the time course data, which we supply as a
pandas.DataFrame - an initial parameter guess
The fitting routine will create data at every time points specified in the DataFrame and compare all of them.
Other than that, the same rules of the steady-state fitting apply.
fit_result = fit.time_course(
model_fn(),
p0={"k1": 1.038, "k2": 1.87, "k3": 1.093},
data=res,
minimizer=fit.LocalScipyMinimizer(),
).unwrap_or_err()
fit_result.best_pars
{'k1': np.float64(1.0000000969916194),
'k2': np.float64(2.000000768975403),
'k3': np.float64(1.0000000183365565)}
Protocol time courses¶
Normally, you would fit your model to experimental data.
Here, again, for the sake of simplicity, we will generate some synthetic data.
protocol = make_protocol(
[
(1, {"k1": 1.0}),
(1, {"k1": 2.0}),
(1, {"k1": 1.0}),
]
)
res_protocol = (
Simulator(model_fn())
.update_parameters({"k1": 1.0, "k2": 2.0, "k3": 1.0})
.simulate_protocol(
protocol,
time_points_per_step=10,
)
.get_result()
.unwrap_or_err()
).get_combined()
fig, ax = plot.lines(res_protocol)
ax.set(xlabel="time / a.u.", ylabel="Conc. & Flux / a.u.")
plt.show()
For the protocol time course fit we need three inputs
- an initial parameter guess
- the time course data, which we supply as a
pandas.DataFrame - the protocol, which we supply as a
pandas.DataFrame
Note that the parameter given by the protocol cannot be fitted anymore
fit_result = fit.protocol_time_course(
model_fn(),
p0={"k2": 1.87, "k3": 1.093}, # note that k1 is given by the protocol
data=res_protocol,
protocol=protocol,
minimizer=fit.LocalScipyMinimizer(),
).unwrap_or_err()
fit_result.best_pars
{'k2': np.float64(1.9999998987832102), 'k3': np.float64(1.000000229655018)}
Ensemble fitting¶
mxlpy supports ensebmle fitting, which is a multi-model single data approach, where shared parameters will be applied to all models at the same time.
Here you supply an iterable of models instead of just one, otherwise the API stays the same.
ensemble_fit = fit.ensemble_steady_state(
[
model_fn(),
model_fn(),
],
data=res.iloc[-1],
p0={"k1": 1.038, "k2": 1.87, "k3": 1.093},
minimizer=fit.LocalScipyMinimizer(tol=1e-6),
)
0%| | 0/2 [00:00<?, ?it/s]
50%|█████ | 1/2 [00:01<00:01, 1.37s/it]
100%|██████████| 2/2 [00:01<00:00, 1.38it/s]
To get the best fitting model, you can use get_best_fit on the ensemble fit
fit_result = ensemble_fit.get_best_fit()
And you can of course also access all other fits
[i.loss for i in ensemble_fit.fits]
[np.float64(7.41294098350708e-05), np.float64(7.41294098350708e-05)]
Time course¶
Time course fits are adjusted just the same
ensemble_fit = fit.ensemble_time_course(
[
model_fn(),
model_fn(),
],
data=res,
p0={"k1": 1.038, "k2": 1.87, "k3": 1.093},
minimizer=fit.LocalScipyMinimizer(tol=1e-6),
)
0%| | 0/2 [00:00<?, ?it/s]
50%|█████ | 1/2 [00:03<00:03, 3.71s/it]
100%|██████████| 2/2 [00:03<00:00, 1.93s/it]
Protocol time course¶
As are protocol time courses
ensemble_fit = fit.ensemble_protocol_time_course(
[
model_fn(),
model_fn(),
],
data=res_protocol,
protocol=protocol,
p0={"k2": 1.87, "k3": 1.093}, # note that k1 is given by the protocol
minimizer=fit.LocalScipyMinimizer(tol=1e-6),
)
0%| | 0/2 [00:00<?, ?it/s]
50%|█████ | 1/2 [00:02<00:02, 2.16s/it]
100%|██████████| 2/2 [00:02<00:00, 1.12s/it]
Joint fitting¶
Next, we support joint fitting, which is a combined multi-model multi-data approach, where shared parameters will be applied to all models at the same time
fit.joint_steady_state(
[
fit.FitSettings(model=model_fn(), data=res.iloc[-1]),
fit.FitSettings(model=model_fn(), data=res.iloc[-1]),
],
p0={"k1": 1.038, "k2": 1.87, "k3": 1.093},
minimizer=fit.LocalScipyMinimizer(tol=1e-6),
)
/home/runner/work/MxlPy/MxlPy/.venv/lib/python3.12/site-packages/scipy/optimize/_numdiff.py:686: RuntimeWarning: invalid value encountered in subtract df = [f_eval - f0 for f_eval in f_evals]
Result(value=JointFit(
best_pars={'k1': np.float64(1.038), 'k2': np.float64(1.87), 'k3': np.float64(1.093)},
loss=np.float64(0.3979583519667012)
))
fit.joint_time_course(
[
fit.FitSettings(model=model_fn(), data=res),
fit.FitSettings(model=model_fn(), data=res),
],
p0={"k1": 1.038, "k2": 1.87, "k3": 1.093},
minimizer=fit.LocalScipyMinimizer(tol=1e-6),
)
Result(value=JointFit(
best_pars={
'k1': np.float64(0.9999999762675598),
'k2': np.float64(2.0000001269164405),
'k3': np.float64(0.9999999033815101)
},
loss=np.float64(1.193140542842726e-06)
))
fit.joint_protocol_time_course(
[
fit.FitSettings(model=model_fn(), data=res_protocol, protocol=protocol),
fit.FitSettings(model=model_fn(), data=res_protocol, protocol=protocol),
],
p0={"k2": 1.87, "k3": 1.093},
minimizer=fit.LocalScipyMinimizer(tol=1e-6),
)
Result(value=JointFit(
best_pars={'k2': np.float64(2.0000002702777744), 'k3': np.float64(0.9999999478771513)},
loss=np.float64(8.073324216620025e-07)
))
Mixed joint fitting¶
Lastly, we support mixed-joint fitting, where each analysis takes it's own residual function to allow fitting both time series and steady-state data for multiple models at the same time.
fit.joint_mixed(
[
fit.MixedSettings(
model=model_fn(),
data=res.iloc[-1],
residual_fn=fit.steady_state_residual,
),
fit.MixedSettings(
model=model_fn(),
data=res,
residual_fn=fit.time_course_residual,
),
fit.MixedSettings(
model=model_fn(),
data=res_protocol,
protocol=protocol,
residual_fn=fit.protocol_time_course_residual,
),
],
p0={"k2": 1.87, "k3": 1.093},
minimizer=fit.LocalScipyMinimizer(tol=1e-6),
)
Result(value=JointFit(
best_pars={'k2': np.float64(1.87), 'k3': np.float64(1.093)},
loss=np.float64(1.1417581457324932)
))
First finish line
With that you now know most of what you will need from a day-to-day basis about fitting in mxlpy.Congratulations!
Advanced topics / customisation¶
All fitting routines internally are build in a way that they will call a tree of functions.
minimizerresidual_fnintegratorloss_fn
You can therefore use dependency injection to overwrite the minimisation function, the loss function, the residual function and the integrator if need be.
from functools import partial
from typing import TYPE_CHECKING, cast
from mxlpy.integrators import Scipy
if TYPE_CHECKING:
import pandas as pd
Parameterising scipy optimise¶
optimizer = fit.LocalScipyMinimizer(tol=1e-6, method="Nelder-Mead")
Custom loss function¶
You can change the loss function that is being passed to the minimsation function using the loss_fn keyword.
Depending on the use case (time course vs steady state) this function will be passed two pandas DataFrames or Series.
def mean_absolute_error(
x: pd.DataFrame | pd.Series,
y: pd.DataFrame | pd.Series,
) -> float:
"""Mean absolute error between two dataframes."""
return cast(float, np.mean(np.abs(x - y)))
(
fit.time_course(
model_fn(),
p0={"k1": 1.038, "k2": 1.87, "k3": 1.093},
data=res,
loss_fn=mean_absolute_error,
minimizer=fit.LocalScipyMinimizer(),
)
.unwrap_or_err()
.best_pars
)
{'k1': np.float64(1.0000000389049177),
'k2': np.float64(2.0000000632887405),
'k3': np.float64(1.0000001178944267)}
Custom integrator¶
You can change the default integrator to an integrator of your choice by partially application of the class of any of the existing ones.
Here, for example, we choose the Scipy solver suite and set the default relative and absolute tolerances to 1e-6 respectively.
(
fit.time_course(
model_fn(),
p0={"k1": 1.038, "k2": 1.87, "k3": 1.093},
data=res,
integrator=partial(Scipy, rtol=1e-6, atol=1e-6),
minimizer=fit.LocalScipyMinimizer(),
)
.unwrap_or_err()
.best_pars
)
{'k1': np.float64(1.0000001588877794),
'k2': np.float64(2.0000005027949905),
'k3': np.float64(1.0000001158480534)}