In [1]:

from __future__ import annotations

from pathlib import Path
from typing import Any

import matplotlib.pyplot as plt

from example_models import get_linear_chain_2v
from modelbase2.types import unwrap, unwrap2


def print_annotated(description: str, value: Any) -> None:
    print(
        description,
        value,
        sep="\n",
        end="\n\n",
    )

from __future__ import annotations from pathlib import Path from typing import Any import matplotlib.pyplot as plt from example_models import get_linear_chain_2v from modelbase2.types import unwrap, unwrap2 def print_annotated(description: str, value: Any) -> None: print( description, value, sep="\n", end="\n\n", )

Model building basics¶

In the following you will learn how to build and simulate your first model using modelbase.

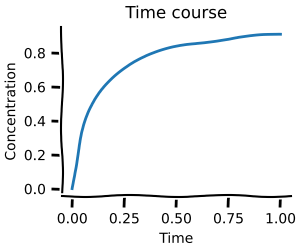
This will allow you to create time courses and do steady-state analysis as shown below.

Defining your first model¶

Let's say you want to model the following chemical network of a linear chain of reactions

$$ \Large \varnothing \xrightarrow{v_0} S \xrightarrow{v_1} P \xrightarrow{v_2} \varnothing $$

We can translate this into a system of ordinary differential equations (ODEs)

$$\begin{align*} \frac{dS}{dt} &= v_0 - v_1 \\ \frac{dP}{dt} &= v_1 - v_2 \\ \end{align*} $$

Note that the rates $v$ effect the variables by certain factors, known as stoichiometries.
We can explicity write out these factors like this:

$$\begin{align*} \frac{dS}{dt} &= 1 \cdot v_0 -1 \cdot v_1 \\ \frac{dP}{dt} &= 1\cdot v_1 -1 \cdot v_2 \\ \end{align*} $$

In the example the stoichiometries are all $1$ or $-1$, however, they can have any real value.
We can write out the stoichiometries using a stoichiometric matrix:

Variable	$v_0$	$v_1$	$v_2$
S	1	-1	0
P	0	1	-1

Which we can read as (ignoring the 0 entries):

• S is produced by $v_0$ and consumed by $v_1$
• P is produced by $v_1$ and consumed by $v_2$

Lastly we choose rate equations for each rate to get the flux vector $v$

$$\begin{align*} v_0 &= k_{in} \\ v_1 &= k_1 * S \\ v_2 &= k_{out} * P \\ \end{align*}$$

Implementing your first model¶

Now let's implement this first model in modelbase.
We start by creating the rate functions $\textbf{v}$.
Note that these should be general and re-usable whenever possible, to make your model clear to people reading it.
Try to give these functions names that are meaningful to your audience, e.g. a rate function k * s could be named proportional or mass-action.

In [2]:

def constant(k: float) -> float:
    return k


def proportional(k: float, s: float) -> float:
    return k * s

def constant(k: float) -> float: return k def proportional(k: float, s: float) -> float: return k * s

Next, we create our model.

For this, we first import the Model class from the modelbase2 package.

In [3]:

from modelbase2 import Model

model = Model()

from modelbase2 import Model model = Model()

We first add parameters to the model using .add_parameters({name: value}).

Note that the function returns our Model object again.
This will be useful later, as we can chain multiple calls together.

In [4]:

model = model.add_parameters({"k_in": 1, "k_1": 1, "k_out": 1})

model = model.add_parameters({"k_in": 1, "k_1": 1, "k_out": 1})

Next we add the dynamic variables S and P with their respective initial condition.

In [5]:

model = model.add_variables({"S": 0, "P": 0})

model = model.add_variables({"S": 0, "P": 0})

Finally, we add the three reactions by using

.add_reaction(
    name,              # the internal name for the reaction
    fn=...,            # a python function to be evaluated
    args=[name, ...]   # the arguments passed to the python function
    stoichiometry={    # a mapping encoding how much the variable `name`
        name: value    # is changed by the reaction
    },
)

Attention
There are a couple of points to note here.
First, the function passed to fn here (and elsewhere) needs to be pickle-able
Thus, lambda functions are not supported!

Second, the arguments defined with args are passed to fn by position, not by name.
Thus, the order of arguments in args needs to match the order of arguments in fn

In [6]:

model.add_reaction(
    "v0",
    fn=constant,
    args=["k_in"],
    stoichiometry={"S": 1},  # produces one S
)
model.add_reaction(
    "v1",
    fn=proportional,
    args=["k_1", "S"],  # note that the order needs to match `proportional`
    stoichiometry={"S": -1, "P": 1},  # consumes one S and produces one P
)
model.add_reaction(
    "v2",
    fn=proportional,
    args=["k_out", "P"],  # note that the order needs to match `proportional`
    stoichiometry={"P": -1},  # exports one P
)

model.add_reaction( "v0", fn=constant, args=["k_in"], stoichiometry={"S": 1}, # produces one S ) model.add_reaction( "v1", fn=proportional, args=["k_1", "S"], # note that the order needs to match `proportional` stoichiometry={"S": -1, "P": 1}, # consumes one S and produces one P ) model.add_reaction( "v2", fn=proportional, args=["k_out", "P"], # note that the order needs to match `proportional` stoichiometry={"P": -1}, # exports one P )

Out[6]:

Model(_ids={'k_in': 'parameter', 'k_1': 'parameter', 'k_out': 'parameter', 'S': 'variable', 'P': 'variable', 'v0': 'reaction', 'v1': 'reaction', 'v2': 'reaction'}, _variables={'S': 0, 'P': 0}, _parameters={'k_in': 1, 'k_1': 1, 'k_out': 1}, _derived={}, _readouts={}, _reactions={'v0': Reaction(fn=<function constant at 0x7f7cadee6980>, stoichiometry={'S': 1}, args=['k_in'], math=None), 'v1': Reaction(fn=<function proportional at 0x7f7cadee6a20>, stoichiometry={'S': -1, 'P': 1}, args=['k_1', 'S'], math=None), 'v2': Reaction(fn=<function proportional at 0x7f7cadee6a20>, stoichiometry={'P': -1}, args=['k_out', 'P'], math=None)}, _surrogates={}, _cache=None)

Note, that we in general recommend to use a single function that returns the model instead of defining it globally.
This allows us to quickly re-create the model whenever we need a fresh version of it.
Below, we define the same model again, but inside a single function.

Note that we made use of operator chaining to avoid having to write model for every call.

So we can write Model.method1().method2()... instead of having to write

model.method1()
model.method2()

etc

In [7]:

def create_linear_chain_model() -> Model:
    return (
        Model()
        .add_parameters({"k_in": 1, "k_1": 1, "k_out": 1})
        .add_variables({"S": 0, "P": 0})
        .add_reaction(
            "v0",
            fn=constant,
            args=["k_in"],
            stoichiometry={"S": 1},  # produces one S
        )
        .add_reaction(
            "v1",
            fn=proportional,
            args=["k_1", "S"],  # note that the order needs to match `proportional`
            stoichiometry={"S": -1, "P": 1},  # consumes one S and produces one P
        )
        .add_reaction(
            "v2",
            fn=proportional,
            args=["k_out", "P"],  # note that the order needs to match `proportional`
            stoichiometry={"P": -1},  # exports one P
        )
    )

def create_linear_chain_model() -> Model: return ( Model() .add_parameters({"k_in": 1, "k_1": 1, "k_out": 1}) .add_variables({"S": 0, "P": 0}) .add_reaction( "v0", fn=constant, args=["k_in"], stoichiometry={"S": 1}, # produces one S ) .add_reaction( "v1", fn=proportional, args=["k_1", "S"], # note that the order needs to match `proportional` stoichiometry={"S": -1, "P": 1}, # consumes one S and produces one P ) .add_reaction( "v2", fn=proportional, args=["k_out", "P"], # note that the order needs to match `proportional` stoichiometry={"P": -1}, # exports one P ) )

We can then simulate the model by passing it to a Simulator and simulate a time series using .simulate(t_end).
Finally, we can obtain the concentrations and fluxes using get_concs_and_fluxes.

While you can directly plot the pd.DataFrames, modelbase supplies a variety of plots in the plot namespace that are worth checking out.

In [8]:

from modelbase2 import Simulator, plot

concs, fluxes = (
    Simulator(create_linear_chain_model())  # initialise the simulator
    .simulate(5)  # simulate until t_end = 5 a.u.
    .get_concs_and_fluxes()  # return pd.DataFrames for concentrations and fluxes
)

if concs is not None and fluxes is not None:
    fig, (ax1, ax2) = plot.two_axes(figsize=(6, 2.5))
    _ = plot.lines(concs, ax=ax1)
    _ = plot.lines(fluxes, ax=ax2)

    # Never forget to labelr you axes :)
    ax1.set(xlabel="time / a.u.", ylabel="concentration / a.u.")
    ax2.set(xlabel="time / a.u.", ylabel="flux / a.u.")
    plt.show()

from modelbase2 import Simulator, plot concs, fluxes = ( Simulator(create_linear_chain_model()) # initialise the simulator .simulate(5) # simulate until t_end = 5 a.u. .get_concs_and_fluxes() # return pd.DataFrames for concentrations and fluxes ) if concs is not None and fluxes is not None: fig, (ax1, ax2) = plot.two_axes(figsize=(6, 2.5)) _ = plot.lines(concs, ax=ax1) _ = plot.lines(fluxes, ax=ax2) # Never forget to labelr you axes :) ax1.set(xlabel="time / a.u.", ylabel="concentration / a.u.") ax2.set(xlabel="time / a.u.", ylabel="flux / a.u.") plt.show()

Note, that we checked whether the results were None in case the simulation failed.
Explicitly checking using an if clause is the prefered error handling mechanism.

If you are sure the simulation won't fail, and still want your code to be type-safe, you can use unwrap and unwrap2. The 2 here just refers to two instead of one arguments.

c = unwrap(Simulator(model).simulate(10).get_concs())
c, v = unwrap2(Simulator(model).simulate(10).get_concs_and_fluxes())

Note that these functions will throw an error if the values are None, which potentially might crash your programs.

Derived quantities¶

Frequently it makes sense to derive one quantity in a model from other quantities.
This can be done for

• parameters derived from other parameters
• variables derived from parameters or other variables
• stoichiometries derived from parameters or variables (more on this later)

modelbase offers a unified interface for derived parameters and variables usign Model.add_derived().

In [9]:

def moiety_1(x1: float, total: float) -> float:
    return total - x1


def model_derived() -> Model:
    return (
        Model()
        .add_variables({"ATP": 1.0})
        .add_parameters({"ATP_total": 1.0, "k_base": 1.0, "e0_atpase": 1.0})
        .add_derived("k_atp", proportional, args=["k_base", "e0_atpase"])
        .add_derived("ADP", moiety_1, args=["ATP", "ATP_total"])
        .add_reaction(
            "ATPase", proportional, args=["k_atp", "ATP"], stoichiometry={"ATP": -1}
        )
    )


concs, fluxes = Simulator(model_derived()).simulate(10).get_full_concs_and_fluxes()
if concs is not None:
    fig, ax = plot.lines(concs)
    ax.set(xlabel="time / a.u.", ylabel="concentration / a.u.")
    plt.show()

def moiety_1(x1: float, total: float) -> float: return total - x1 def model_derived() -> Model: return ( Model() .add_variables({"ATP": 1.0}) .add_parameters({"ATP_total": 1.0, "k_base": 1.0, "e0_atpase": 1.0}) .add_derived("k_atp", proportional, args=["k_base", "e0_atpase"]) .add_derived("ADP", moiety_1, args=["ATP", "ATP_total"]) .add_reaction( "ATPase", proportional, args=["k_atp", "ATP"], stoichiometry={"ATP": -1} ) ) concs, fluxes = Simulator(model_derived()).simulate(10).get_full_concs_and_fluxes() if concs is not None: fig, ax = plot.lines(concs) ax.set(xlabel="time / a.u.", ylabel="concentration / a.u.") plt.show()

Introspection¶

If the simulation didn't show the expected results, it is usually a good idea to try to pinpoint the error.
modelbase offers a variety of methods to access intermediate results.

The first is to check whether all derived quantities were calculate correctly.
For this, you can use the get_args method, which is named consistently with the args argument in all methods like add_reaction.

In [10]:

m = create_linear_chain_model()

print_annotated(
    "Using initial conditions as default:",
    m.get_args(),
)

print_annotated(
    "Using custom concentrations:",
    m.get_args({"S": 1.0, "P": 0.5}),
)

m = create_linear_chain_model() print_annotated( "Using initial conditions as default:", m.get_args(), ) print_annotated( "Using custom concentrations:", m.get_args({"S": 1.0, "P": 0.5}), )

Using initial conditions as default:
k_in     1.0
k_1      1.0
k_out    1.0
S        0.0
P        0.0
time     0.0
dtype: float64

Using custom concentrations:
k_in     1.0
k_1      1.0
k_out    1.0
S        1.0
P        0.5
time     0.0
dtype: float64

If the args look fine, the next step is usually to check whether the rate equations are looking as expected

In [11]:

m = create_linear_chain_model()
print_annotated(
    "Using initial conditions as default:",
    m.get_fluxes(),
)
print_annotated(
    "Using custom concentrations:",
    m.get_fluxes({"S": 1.0, "P": 0.5}),
)

m = create_linear_chain_model() print_annotated( "Using initial conditions as default:", m.get_fluxes(), ) print_annotated( "Using custom concentrations:", m.get_fluxes({"S": 1.0, "P": 0.5}), )

Using initial conditions as default:
v0    1.0
v1    0.0
v2    0.0
dtype: float64

Using custom concentrations:
v0    1.0
v1    1.0
v2    0.5
dtype: float64

and whether the stoichiometries are assigned correctly

In [12]:

m = create_linear_chain_model()
m.get_stoichiometries()

m = create_linear_chain_model() m.get_stoichiometries()

Out[12]:

	v0	v1	v2
S	1.0	-1.0	0.0
P	0.0	1.0	-1.0

Lastly, you can check the generated right hand side

In [13]:

m = create_linear_chain_model()

print_annotated(
    "Using initial conditions as default:",
    m.get_right_hand_side(),
)

print_annotated(
    "Using custom concentrations:",
    m.get_right_hand_side({"S": 1.0, "P": 0.5}),
)

m = create_linear_chain_model() print_annotated( "Using initial conditions as default:", m.get_right_hand_side(), ) print_annotated( "Using custom concentrations:", m.get_right_hand_side({"S": 1.0, "P": 0.5}), )

Using initial conditions as default:
S    1.0
P    0.0
dtype: float64

Using custom concentrations:
S    0.0
P    0.5
dtype: float64

If any of the quantities above were unexpected, you can check the model interactively by accessing the various collections.

Note: the returned quantities are copies of the internal data, modifying these won't have any effect on the model

In [14]:

print_annotated("Parameters", m.parameters)
print_annotated("Variables", m.variables)
print_annotated("Reactions", m.reactions)

print_annotated("Parameters", m.parameters) print_annotated("Variables", m.variables) print_annotated("Reactions", m.reactions)

Parameters
{'k_in': 1, 'k_1': 1, 'k_out': 1}

Variables
{'S': 0, 'P': 0}

Reactions
{'v0': Reaction(fn=<function constant at 0x7f7cadee6980>, stoichiometry={'S': 1}, args=['k_in'], math=None), 'v1': Reaction(fn=<function proportional at 0x7f7cadee6a20>, stoichiometry={'S': -1, 'P': 1}, args=['k_1', 'S'], math=None), 'v2': Reaction(fn=<function proportional at 0x7f7cadee6a20>, stoichiometry={'P': -1}, args=['k_out', 'P'], math=None)}

In case you model contains derived quantitites you can access the derived quantities using .derived.
Note that this returns a copy of the derived quantities, so editing it won't have any effect on the model.

In [15]:

model_derived().derived

model_derived().derived

Out[15]:

{'k_atp': Derived(fn=<function proportional at 0x7f7cadee6a20>, args=['k_base', 'e0_atpase'], math=None),
 'ADP': Derived(fn=<function moiety_1 at 0x7f7cade42ac0>, args=['ATP', 'ATP_total'], math=None)}

CRUD¶

The model has a complete create, read, update, delete API for all it's elements.
The methods and attributes are named consistenly, with add instead of create and get instead of read.
Note that the elements itself are accessible as properties, e.g. .parameters which will return copies of the data.
Only use the supplied methods to change the internal state of the model.

Here are some example methods and attributes for parameters

Functionality	Parameters
Create	.add_parameter(), .add_parameters()
Read	.parameters, .get_parameter_names()
Update	.update_parameter(), .update_parameters(), .scale_parameter(), scale.parameters()
Delete	.remove_parameter(), .remove_parameters()

and variables

Functionality	Variables
Create	.add_variable(), .add_variables()
Read	.variables, .get_variable_names(), get_initial_conditions()
Update	.update_variable(), .update_variables()
Delete	.remove_parameter(), .remove_parameters()

In [16]:

m = create_linear_chain_model()

# Calculate fluxes
print_annotated(
    "Before update",
    m.get_fluxes({"S": 1.0, "P": 0.5}),
)

# Update parameters
m.update_parameters({"k_in": 2.0})

# Calculate fluxes again
print_annotated(
    "After update",
    m.get_fluxes({"S": 1.0, "P": 0.5}),
)

m = create_linear_chain_model() # Calculate fluxes print_annotated( "Before update", m.get_fluxes({"S": 1.0, "P": 0.5}), ) # Update parameters m.update_parameters({"k_in": 2.0}) # Calculate fluxes again print_annotated( "After update", m.get_fluxes({"S": 1.0, "P": 0.5}), )

Before update
v0    1.0
v1    1.0
v2    0.5
dtype: float64

After update
v0    2.0
v1    1.0
v2    0.5
dtype: float64

Derived stoichiometries¶

To define derived stoichiometries you need to use the Derived class as a value in the stoichiometries.

So instead of defining them like this

stoichiometry={"x": 1.0}

you use the Derived class as the value

stoichiometry={"x": Derived(constant, args=["stoich"])}

In [17]:

from modelbase2 import Derived

concs, fluxes = unwrap2(
    Simulator(
        Model()
        .add_parameters({"stoich": -1.0, "k": 1.0})
        .add_variables({"x": 1.0})
        .add_reaction(
            "name",
            proportional,
            args=["x", "k"],
            # Define derived stoichiometry here
            stoichiometry={"x": Derived(constant, args=["stoich"])},
        )
    )
    .simulate(1)
    # Update parameter the derived stoichiometry depends on
    .update_parameter("stoich", -4.0)
    # Continue simulation
    .simulate(5)
    .get_concs_and_fluxes()
)

_, ax = plot.lines(concs)
ax.set(xlabel="time / a.u.", ylabel="concentration / a.u.")
plt.show()

from modelbase2 import Derived concs, fluxes = unwrap2( Simulator( Model() .add_parameters({"stoich": -1.0, "k": 1.0}) .add_variables({"x": 1.0}) .add_reaction( "name", proportional, args=["x", "k"], # Define derived stoichiometry here stoichiometry={"x": Derived(constant, args=["stoich"])}, ) ) .simulate(1) # Update parameter the derived stoichiometry depends on .update_parameter("stoich", -4.0) # Continue simulation .simulate(5) .get_concs_and_fluxes() ) _, ax = plot.lines(concs) ax.set(xlabel="time / a.u.", ylabel="concentration / a.u.") plt.show()

Simulations: time courses¶

Time courses are simulations over time

You can obtain the time course of integration using the simulate method.
There are two ways how you can define the time points this function returns.

1. supply the end time t_end
2. supply both end time and number of steps with t_end and steps

If you want to set the exact time points to be returned use simulate_time_course

simulate(t_end=10)
simulate(t_end=10, steps=10)
simulate_time_course(np.linspace(0, 10, 11))

In [18]:

concs, fluxes = unwrap2(
    Simulator(get_linear_chain_2v())
    .simulate(t_end=10)  # simulate until t_end = 10 a.u.
    .get_concs_and_fluxes()
)

fig, ax = plot.lines(concs)
ax.set(xlabel="time / a.u.", ylabel="concentration / a.u.")
plt.show()

concs, fluxes = unwrap2( Simulator(get_linear_chain_2v()) .simulate(t_end=10) # simulate until t_end = 10 a.u. .get_concs_and_fluxes() ) fig, ax = plot.lines(concs) ax.set(xlabel="time / a.u.", ylabel="concentration / a.u.") plt.show()

By default, the Simulator is initialised with the initial concentrations set in the Model.
Optionally, you can overwrite the initial conditions using the y0 argument.

Simulator(model, y0={name: value, ...})

In [19]:

concs, fluxes = unwrap2(
    Simulator(create_linear_chain_model(), y0={"S": 2.0, "P": 0.0})
    .simulate(10)
    .get_concs_and_fluxes()
)

fig, (ax1, ax2) = plot.two_axes(figsize=(6, 3))
_ = plot.lines(concs, ax=ax1)
_ = plot.lines(fluxes, ax=ax2)

ax1.set(xlabel="time / a.u.", ylabel="concentration / a.u.")
ax2.set(xlabel="time / a.u.", ylabel="flux / a.u.")
plt.show()

concs, fluxes = unwrap2( Simulator(create_linear_chain_model(), y0={"S": 2.0, "P": 0.0}) .simulate(10) .get_concs_and_fluxes() ) fig, (ax1, ax2) = plot.two_axes(figsize=(6, 3)) _ = plot.lines(concs, ax=ax1) _ = plot.lines(fluxes, ax=ax2) ax1.set(xlabel="time / a.u.", ylabel="concentration / a.u.") ax2.set(xlabel="time / a.u.", ylabel="flux / a.u.") plt.show()

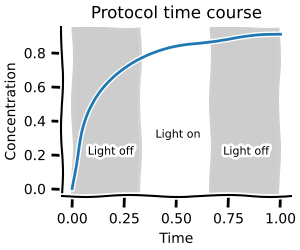
Simulations: protocol time course¶

Protocols are used to make parameter changes discrete in time, such as turning a light on and off.
This is useful reproducing experimental time courses where a parameter was changed at fixed time points.

The protocol is defined as a pandas.DataFrame using pd.Timedelta values as in index, and the parameter values at the respective time interval as values.

pd.Timedelta	p1	p2
0 days 00:00:01	1	0
0 days 00:00:03	2	1
0 days 00:00:06	1	2

You can use as many parameters as you want.

Note
modelbase assigns one second of the Timedelta to one time unit of the integration.
modelbase does not take into account whether your integration might use a different time unit.

For convenience, we supply the make_protocol function, which takes in a pair of the duration of the time-step on the respective parameter values.

In [20]:

from modelbase2 import make_protocol

protocol = make_protocol(
    [
        (1, {"k1": 1}),  # for one second value of 1
        (2, {"k1": 2}),  # for two seconds value of 2
        (3, {"k1": 1}),  # for three seconds value of 1
    ]
)
protocol

from modelbase2 import make_protocol protocol = make_protocol( [ (1, {"k1": 1}), # for one second value of 1 (2, {"k1": 2}), # for two seconds value of 2 (3, {"k1": 1}), # for three seconds value of 1 ] ) protocol

Out[20]:

	k1
Timedelta
0 days 00:00:01	1
0 days 00:00:03	2
0 days 00:00:06	1

Now instead of running simulate or simulate_time_course we use simulate_over_protocol

In [21]:

concs, fluxes = unwrap2(
    Simulator(get_linear_chain_2v())
    .simulate_over_protocol(protocol)
    .get_concs_and_fluxes()
)

fig, ax = plt.subplots()
plot.lines(concs, ax=ax)
plot.shade_protocol(protocol["k1"], ax=ax, alpha=0.1)
ax.set(xlabel="time / a.u.", ylabel="concentration / a.u.")
plt.show()

concs, fluxes = unwrap2( Simulator(get_linear_chain_2v()) .simulate_over_protocol(protocol) .get_concs_and_fluxes() ) fig, ax = plt.subplots() plot.lines(concs, ax=ax) plot.shade_protocol(protocol["k1"], ax=ax, alpha=0.1) ax.set(xlabel="time / a.u.", ylabel="concentration / a.u.") plt.show()

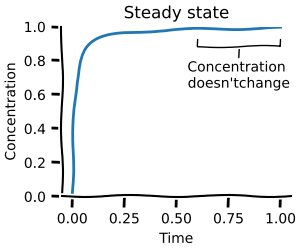
Simulations: steady-state¶

A steady-state describes a state at which the concentrations of the system don't change anymore (also called fixed points).

You can simulate until the model reaches a steady-state using the simulate_to_steady_state method.

In [22]:

concs, fluxes = unwrap2(
    Simulator(get_linear_chain_2v())  # optionally supply initial conditions
    .simulate_to_steady_state()
    .get_concs_and_fluxes()
)

fig, ax = plot.bars(concs)
ax.set(xlabel="Variable / a.u.", ylabel="Concentration / a.u.")
plt.show()

concs, fluxes = unwrap2( Simulator(get_linear_chain_2v()) # optionally supply initial conditions .simulate_to_steady_state() .get_concs_and_fluxes() ) fig, ax = plot.bars(concs) ax.set(xlabel="Variable / a.u.", ylabel="Concentration / a.u.") plt.show()

SBML¶

The systems biology markup language (SBML) is a widely used file format for sharing models between different software packages and programming languages.

modelbase2 supports reading and writing sbml models using the sbml.read and sbml.write functions.

In [23]:

from modelbase2 import sbml

model = sbml.read(Path("assets") / "00001-sbml-l3v2.xml")
concs, fluxes = unwrap2(Simulator(model).simulate(10).get_concs_and_fluxes())
_ = plot.lines(concs)

from modelbase2 import sbml model = sbml.read(Path("assets") / "00001-sbml-l3v2.xml") concs, fluxes = unwrap2(Simulator(model).simulate(10).get_concs_and_fluxes()) _ = plot.lines(concs)

When exporting a model, you can supply additional meta-information like units and compartmentalisation.
See the official sbml documentation for more information of legal values.

In [24]:

sbml.write(
    model,
    file=Path(".cache") / "model.xml",
    extent_units="mole",
    substance_units="mole",
    time_units="second",
)

sbml.write( model, file=Path(".cache") / "model.xml", extent_units="mole", substance_units="mole", time_units="second", )

Out[24]:

PosixPath('.cache/model.xml')

First finish line

With that you now know most of what you will need from a day-to-day basis about model building and simulation in modelbase2.

Congratulations!

Advanced topics¶

Time-dependent reactions¶

You can use the special name time to refer to the actual integration time in the rare case a reaction or module depends on it explicitly.
This is why the methods get_args, get_fluxes etc. also take an additional time argument.

In [25]:

def time_dependency() -> Model:
    return (
        Model()
        .add_variable("x", 1.0)
        .add_reaction(
            "v1",
            proportional,
            args=["time", "x"],
            stoichiometry={"x": -1},
        )
    )


model = time_dependency()

# Watch our for explicit time dependency here!
print_annotated(
    "Fluxes at time = 1.0",
    model.get_fluxes(time=1.0),
)
print_annotated(
    "Fluxes at time = 2.0",
    model.get_fluxes(time=2.0),
)

# During simulations the time is automatically taken care of
_ = unwrap(Simulator(model).simulate(t_end=10).get_concs()).plot(
    xlabel="time / a.u.",
    ylabel="amount / a.u.",
    title="Time-dependent reaction",
)

def time_dependency() -> Model: return ( Model() .add_variable("x", 1.0) .add_reaction( "v1", proportional, args=["time", "x"], stoichiometry={"x": -1}, ) ) model = time_dependency() # Watch our for explicit time dependency here! print_annotated( "Fluxes at time = 1.0", model.get_fluxes(time=1.0), ) print_annotated( "Fluxes at time = 2.0", model.get_fluxes(time=2.0), ) # During simulations the time is automatically taken care of _ = unwrap(Simulator(model).simulate(t_end=10).get_concs()).plot( xlabel="time / a.u.", ylabel="amount / a.u.", title="Time-dependent reaction", )

Fluxes at time = 1.0
v1    1.0
dtype: float64

Fluxes at time = 2.0
v1    2.0
dtype: float64

Derived parameters and variables¶

Internally modelbase differentiates between derived parameters and derived variables.
This differentiation is just-in-time before any calculation and thus might change if you change the nature of a parameter / variable.

If you are interested in which category modelbase has placed the derived quantities, you can access .derived_parameters and .derived_variables as well.

In [26]:

def model_derived() -> Model:
    return (
        Model()
        .add_variables({"ATP": 1.0})
        .add_parameters({"ATP_total": 1.0, "k_base": 1.0, "e0_atpase": 1.0})
        .add_derived("k_atp", proportional, args=["k_base", "e0_atpase"])
        .add_derived("ADP", moiety_1, args=["ATP", "ATP_total"])
        .add_reaction(
            "ATPase", proportional, args=["k_atp", "ATP"], stoichiometry={"ATP": -1}
        )
    )


m = Model().add_parameters({"x1": 1.0}).add_derived("x1d", constant, args=["x1"])
print("Derived Parameters:", m.derived_parameters)
print("Derived Variables:", m.derived_variables)

print("\nMaking x1 dynamic")
m.make_parameter_dynamic("x1")
print("Derived Parameters:", m.derived_parameters)
print("Derived Variables:", m.derived_variables)

def model_derived() -> Model: return ( Model() .add_variables({"ATP": 1.0}) .add_parameters({"ATP_total": 1.0, "k_base": 1.0, "e0_atpase": 1.0}) .add_derived("k_atp", proportional, args=["k_base", "e0_atpase"]) .add_derived("ADP", moiety_1, args=["ATP", "ATP_total"]) .add_reaction( "ATPase", proportional, args=["k_atp", "ATP"], stoichiometry={"ATP": -1} ) ) m = Model().add_parameters({"x1": 1.0}).add_derived("x1d", constant, args=["x1"]) print("Derived Parameters:", m.derived_parameters) print("Derived Variables:", m.derived_variables) print("\nMaking x1 dynamic") m.make_parameter_dynamic("x1") print("Derived Parameters:", m.derived_parameters) print("Derived Variables:", m.derived_variables)

Derived Parameters: {'x1d': Derived(fn=<function constant at 0x7f7cadee6980>, args=['x1'], math=None)}
Derived Variables: {}

Making x1 dynamic
Derived Parameters: {}
Derived Variables: {'x1d': Derived(fn=<function constant at 0x7f7cadee6980>, args=['x1'], math=None)}

Integrator configuration¶

You can explicitly control which integrator is used for the simulations.
As all integrators have different settings, changing them is done on the integrator object itself, which can be found at Simulator().integrator.

By default, the Assimulo integrator is used.
However, that package currenlty requires installation via conda-forge.
If modelbase2 was installed from pypi, this package is not available and modelbase2 will fall back to the Scipy package.
Thus, when setting integrator settings you should always check which integrator you are actually working with, as this otherwise might lead bugs on other systems.

In [27]:

from functools import partial

from modelbase2.integrators import Scipy

model = get_linear_chain_2v()

# You can explicitly set an integrator for the simulation
s = Simulator(model, integrator=Scipy)

# You can also change the default settings of each integrator
s = Simulator(model, integrator=partial(Scipy, atol=1e-6, rtol=1e-6))
s.simulate(5)

# You can also change integration settings mid simulation
# As not all integrators have the same settings, we recommend explicitly checking
# which integrator is currently set
if isinstance(s.integrator, Scipy):
    s.integrator.atol = 1e-6
    s.integrator.rtol = 1e-6
s.simulate(10)
s.get_results().plot()

from functools import partial from modelbase2.integrators import Scipy model = get_linear_chain_2v() # You can explicitly set an integrator for the simulation s = Simulator(model, integrator=Scipy) # You can also change the default settings of each integrator s = Simulator(model, integrator=partial(Scipy, atol=1e-6, rtol=1e-6)) s.simulate(5) # You can also change integration settings mid simulation # As not all integrators have the same settings, we recommend explicitly checking # which integrator is currently set if isinstance(s.integrator, Scipy): s.integrator.atol = 1e-6 s.integrator.rtol = 1e-6 s.simulate(10) s.get_results().plot()

Out[27]:

<Axes: >