In [1]:
Copied!
from __future__ import annotations
from functools import partial
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from example_models.linear_chain import get_linear_chain_2v
from modelbase2 import Model, Simulator, npe, plot, scan
from modelbase2.distributions import LogNormal, Normal, sample
from modelbase2.surrogates import train_polynomial_surrogate, train_torch_surrogate
from modelbase2.types import AbstractSurrogate, unwrap, unwrap2
from __future__ import annotations
from functools import partial
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from example_models.linear_chain import get_linear_chain_2v
from modelbase2 import Model, Simulator, npe, plot, scan
from modelbase2.distributions import LogNormal, Normal, sample
from modelbase2.surrogates import train_polynomial_surrogate, train_torch_surrogate
from modelbase2.types import AbstractSurrogate, unwrap, unwrap2
Mechanistic Learning¶
Mechanistic learning is the intersection of mechanistic modelling and machine learning.
modelbase currently supports two such approaches: surrogates and neural posterior estimation.
In the following we will mostly use the modelbase2.surrogates and modelbase2.npe modules to learn about both approaches.
Surrogate models¶
Surrogate models replace whole parts of a mechanistic model (or even the entire model) with machine learning models.
This allows combining together multiple models of arbitrary size, without having to worry about the internal state of each model.
They are especially useful for improving the description of boundary effects, e.g. a dynamic description of downstream consumption.
We will start with a simple linear chain model
$$ \Large \varnothing \xrightarrow{v_1} x \xrightarrow{v_2} y \xrightarrow{v_3} \varnothing $$
where we want to read out the steady-state rate of $v_3$ dependent on the fixed concentration of $x$, while ignoring the inner state of the model.
$$ \Large x \xrightarrow{} ... \xrightarrow{v_3}$$
Since we need to fix a variable as an parameter, we can use the make_variable_static method to do that.
In [2]:
Copied!
# Now "x" is a parameter
get_linear_chain_2v().make_variable_static("x").parameters
# Now "x" is a parameter
get_linear_chain_2v().make_variable_static("x").parameters
Out[2]:
{'k1': 1.0, 'k2': 2.0, 'k3': 1.0, 'x': 1.0}
And we can already create a function to create a model, which will take our surrogate as an input.
In [3]:
Copied!
def get_model_with_surrogate(surrogate: AbstractSurrogate) -> Model:
model = Model()
model.add_variables({"x": 1.0, "z": 0.0})
# Adding the surrogate
model.add_surrogate(
"surrogate",
surrogate,
args=["x"],
stoichiometries={
"v2": {"x": -1, "z": 1},
},
)
# Note that besides the surrogate we haven't defined any other reaction!
# We could have though
return model
def get_model_with_surrogate(surrogate: AbstractSurrogate) -> Model:
model = Model()
model.add_variables({"x": 1.0, "z": 0.0})
# Adding the surrogate
model.add_surrogate(
"surrogate",
surrogate,
args=["x"],
stoichiometries={
"v2": {"x": -1, "z": 1},
},
)
# Note that besides the surrogate we haven't defined any other reaction!
# We could have though
return model
Create data¶
The surrogates used in the following will all use the steady-state fluxes depending on the inputs.
We can thus create the necessary training data usign scan.steady_state.
Since this is usually a large amount of data, we recommend caching the results using Cache.
In [4]:
Copied!
surrogate_features = pd.DataFrame({"x": np.geomspace(1e-12, 2.0, 21)})
surrogate_targets = scan.steady_state(
get_linear_chain_2v().make_variable_static("x"),
parameters=surrogate_features,
).fluxes.loc[:, ["v3"]]
# It's always a good idea to check the inputs and outputs
fig, (ax1, ax2) = plot.two_axes(figsize=(6, 3), sharex=False)
_ = plot.violins(surrogate_features, ax=ax1)[1].set(
title="Features", ylabel="Flux / a.u."
)
_ = plot.violins(surrogate_targets, ax=ax2)[1].set(
title="Targets", ylabel="Flux / a.u."
)
plt.show()
surrogate_features = pd.DataFrame({"x": np.geomspace(1e-12, 2.0, 21)})
surrogate_targets = scan.steady_state(
get_linear_chain_2v().make_variable_static("x"),
parameters=surrogate_features,
).fluxes.loc[:, ["v3"]]
# It's always a good idea to check the inputs and outputs
fig, (ax1, ax2) = plot.two_axes(figsize=(6, 3), sharex=False)
_ = plot.violins(surrogate_features, ax=ax1)[1].set(
title="Features", ylabel="Flux / a.u."
)
_ = plot.violins(surrogate_targets, ax=ax2)[1].set(
title="Targets", ylabel="Flux / a.u."
)
plt.show()
0%| | 0/21 [00:00<?, ?it/s]
24%|██▍ | 5/21 [00:00<00:00, 47.50it/s]
100%|██████████| 21/21 [00:00<00:00, 85.48it/s]
Polynomial surrogate¶
We can train our polynomial surrogate using train_polynomial_surrogate.
By default this will train polynomials for the degrees (1, 2, 3, 4, 5, 6, 7), but you can change that by using the degrees argument.
The function returns the trained surrogate and the training information for the different polynomial degrees.
Currently the polynomial surrogates are limited to a single feature and a single target
In [5]:
Copied!
surrogate, info = train_polynomial_surrogate(
surrogate_features["x"],
surrogate_targets["v3"],
)
print("Model", surrogate.model, end="\n\n")
print(info["score"])
surrogate, info = train_polynomial_surrogate(
surrogate_features["x"],
surrogate_targets["v3"],
)
print("Model", surrogate.model, end="\n\n")
print(info["score"])
Model 2.0 + 2.0·(-1.0 + 1.0x) degree 1 2.0 2 4.0 3 6.0 4 8.0 5 10.0 6 12.0 7 14.0 Name: score, dtype: float64
You can then insert the surrogate into the model using the function we defined earlier
In [6]:
Copied!
concs, fluxes = unwrap2(
Simulator(get_model_with_surrogate(surrogate))
.simulate(10)
.get_full_concs_and_fluxes()
)
fig, (ax1, ax2) = plot.two_axes(figsize=(8, 3))
plot.lines(concs, ax=ax1)
plot.lines(fluxes, ax=ax2)
ax1.set(xlabel="time / a.u.", ylabel="concentration / a.u.")
ax2.set(xlabel="time / a.u.", ylabel="flux / a.u.")
plt.show()
concs, fluxes = unwrap2(
Simulator(get_model_with_surrogate(surrogate))
.simulate(10)
.get_full_concs_and_fluxes()
)
fig, (ax1, ax2) = plot.two_axes(figsize=(8, 3))
plot.lines(concs, ax=ax1)
plot.lines(fluxes, ax=ax2)
ax1.set(xlabel="time / a.u.", ylabel="concentration / a.u.")
ax2.set(xlabel="time / a.u.", ylabel="flux / a.u.")
plt.show()
While polynomial regression can model nonlinear relationships between variables, it often struggles when the underlying relationship is more complex than a polynomial function.
You will learn about using neural networks in the next section.
Neural network surrogate using PyTorch¶
Neural networks are designed to capture highly complex and nonlinear relationships.
Through layers of neurons and activation functions, neural networks can learn intricate patterns that are not easily represented by e.g. a polynomial.
They have the flexibility to approximate any continuous function, given sufficient depth and appropriate training.
You can train a neural network surrogate based on the popular PyTorch library using train_torch_surrogate.
That function takes the features, targets and the number of epochs as inputs for it's training.
train_torch_surrogate returns the trained surrogate, as well as the training loss.
It is always a good idea to check whether that training loss approaches 0.
In [7]:
Copied!
surrogate, loss = train_torch_surrogate(
features=surrogate_features,
targets=surrogate_targets,
epochs=250,
)
ax = loss.plot(ax=plt.subplots(figsize=(4, 2.5))[1])
ax.set_ylim(0, None)
plt.show()
surrogate, loss = train_torch_surrogate(
features=surrogate_features,
targets=surrogate_targets,
epochs=250,
)
ax = loss.plot(ax=plt.subplots(figsize=(4, 2.5))[1])
ax.set_ylim(0, None)
plt.show()
0%| | 0/250 [00:00<?, ?it/s]
64%|██████▎ | 159/250 [00:00<00:00, 1581.02it/s]
100%|██████████| 250/250 [00:00<00:00, 1588.65it/s]
As before, you can then insert the surrogate into the model using the function we defined earlier
In [8]:
Copied!
concs, fluxes = unwrap2(
Simulator(get_model_with_surrogate(surrogate))
.simulate(10)
.get_full_concs_and_fluxes()
)
fig, (ax1, ax2) = plot.two_axes(figsize=(8, 3))
plot.lines(concs, ax=ax1)
plot.lines(fluxes, ax=ax2)
ax1.set(xlabel="time / a.u.", ylabel="concentration / a.u.")
ax2.set(xlabel="time / a.u.", ylabel="flux / a.u.")
plt.show()
concs, fluxes = unwrap2(
Simulator(get_model_with_surrogate(surrogate))
.simulate(10)
.get_full_concs_and_fluxes()
)
fig, (ax1, ax2) = plot.two_axes(figsize=(8, 3))
plot.lines(concs, ax=ax1)
plot.lines(fluxes, ax=ax2)
ax1.set(xlabel="time / a.u.", ylabel="concentration / a.u.")
ax2.set(xlabel="time / a.u.", ylabel="flux / a.u.")
plt.show()
Troubleshooting¶
It often can make sense to check specific predictions of the surrogate.
For example, what does it predict when the inputs are all 0?
In [9]:
Copied!
print(surrogate.predict(np.array([-0.1])))
print(surrogate.predict(np.array([0.0])))
print(surrogate.predict(np.array([0.1])))
print(surrogate.predict(np.array([-0.1])))
print(surrogate.predict(np.array([0.0])))
print(surrogate.predict(np.array([0.1])))
{'v2': np.float32(-0.008462121)}
{'v2': np.float32(0.0010542409)}
{'v2': np.float32(0.19794546)}
Neural posterior estimation¶
Neural posterior estimation answers the question: what parameters could have generated the data I measured?
Here you use an ODE model and prior knowledge about the parameters of interest to create synthetic data.
You then use the generated synthetic data as the features and the input parameters as the targets to train an inverse problem.
Once that training is successful, the neural network can now predict the input parameters for real world data.
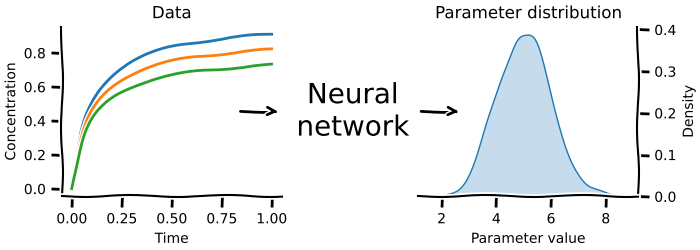
You can use this technique for both steady-state as well as time course data.
The only difference is in using scan.time_course.
Take care here to save the targets as well in case you use cached data :)
In [10]:
Copied!
# Note that now the parameters are the targets
npe_targets = sample(
{
"k1": LogNormal(mean=1.0, sigma=0.3),
},
n=1_000,
)
# And the generated data are the features
npe_features = scan.steady_state(
get_linear_chain_2v(),
parameters=npe_targets,
).results.loc[:, ["y", "v2", "v3"]]
# It's always a good idea to check the inputs and outputs
fig, (ax1, ax2) = plot.two_axes(figsize=(6, 3), sharex=False)
_ = plot.violins(npe_features, ax=ax1)[1].set(title="Features", ylabel="Flux / a.u.")
_ = plot.violins(npe_targets, ax=ax2)[1].set(title="Targets", ylabel="Flux / a.u.")
plt.show()
# Note that now the parameters are the targets
npe_targets = sample(
{
"k1": LogNormal(mean=1.0, sigma=0.3),
},
n=1_000,
)
# And the generated data are the features
npe_features = scan.steady_state(
get_linear_chain_2v(),
parameters=npe_targets,
).results.loc[:, ["y", "v2", "v3"]]
# It's always a good idea to check the inputs and outputs
fig, (ax1, ax2) = plot.two_axes(figsize=(6, 3), sharex=False)
_ = plot.violins(npe_features, ax=ax1)[1].set(title="Features", ylabel="Flux / a.u.")
_ = plot.violins(npe_targets, ax=ax2)[1].set(title="Targets", ylabel="Flux / a.u.")
plt.show()
0%| | 0/1000 [00:00<?, ?it/s]
1%| | 9/1000 [00:00<00:12, 78.00it/s]
2%|▎ | 25/1000 [00:00<00:08, 118.75it/s]
4%|▍ | 42/1000 [00:00<00:06, 139.59it/s]
6%|▌ | 57/1000 [00:00<00:06, 136.33it/s]
7%|▋ | 72/1000 [00:00<00:06, 138.01it/s]
9%|▉ | 88/1000 [00:00<00:06, 140.27it/s]
10%|█ | 104/1000 [00:00<00:06, 143.57it/s]
12%|█▏ | 119/1000 [00:00<00:06, 145.41it/s]
14%|█▎ | 135/1000 [00:00<00:05, 146.12it/s]
15%|█▌ | 151/1000 [00:01<00:05, 146.25it/s]
17%|█▋ | 167/1000 [00:01<00:05, 147.31it/s]
18%|█▊ | 183/1000 [00:01<00:05, 148.32it/s]
20%|█▉ | 198/1000 [00:01<00:05, 138.32it/s]
22%|██▏ | 215/1000 [00:01<00:05, 146.61it/s]
23%|██▎ | 230/1000 [00:01<00:05, 144.32it/s]
25%|██▍ | 248/1000 [00:01<00:04, 153.39it/s]
26%|██▋ | 264/1000 [00:01<00:04, 153.19it/s]
28%|██▊ | 280/1000 [00:01<00:04, 150.99it/s]
30%|██▉ | 296/1000 [00:02<00:04, 148.74it/s]
31%|███ | 312/1000 [00:02<00:04, 147.64it/s]
33%|███▎ | 328/1000 [00:02<00:04, 146.34it/s]
34%|███▍ | 344/1000 [00:02<00:04, 147.34it/s]
36%|███▌ | 360/1000 [00:02<00:04, 150.44it/s]
38%|███▊ | 376/1000 [00:02<00:04, 150.96it/s]
39%|███▉ | 392/1000 [00:02<00:04, 148.32it/s]
41%|████ | 407/1000 [00:02<00:04, 147.75it/s]
42%|████▏ | 423/1000 [00:02<00:03, 150.56it/s]
44%|████▍ | 439/1000 [00:03<00:03, 150.01it/s]
46%|████▌ | 455/1000 [00:03<00:03, 151.30it/s]
47%|████▋ | 471/1000 [00:03<00:03, 152.53it/s]
49%|████▊ | 487/1000 [00:03<00:03, 152.82it/s]
50%|█████ | 503/1000 [00:03<00:03, 153.16it/s]
52%|█████▏ | 519/1000 [00:03<00:03, 152.00it/s]
54%|█████▎ | 535/1000 [00:03<00:03, 151.55it/s]
55%|█████▌ | 551/1000 [00:03<00:02, 151.01it/s]
57%|█████▋ | 567/1000 [00:03<00:02, 152.83it/s]
58%|█████▊ | 583/1000 [00:03<00:02, 152.40it/s]
60%|█████▉ | 599/1000 [00:04<00:02, 149.52it/s]
62%|██████▏ | 616/1000 [00:04<00:02, 152.92it/s]
63%|██████▎ | 632/1000 [00:04<00:02, 148.86it/s]
65%|██████▍ | 647/1000 [00:04<00:02, 145.60it/s]
66%|██████▋ | 663/1000 [00:04<00:02, 144.40it/s]
68%|██████▊ | 679/1000 [00:04<00:02, 148.07it/s]
70%|██████▉ | 695/1000 [00:04<00:02, 150.09it/s]
71%|███████ | 712/1000 [00:04<00:01, 153.14it/s]
73%|███████▎ | 730/1000 [00:04<00:01, 153.84it/s]
75%|███████▍ | 746/1000 [00:05<00:01, 153.02it/s]
76%|███████▌ | 762/1000 [00:05<00:01, 152.10it/s]
78%|███████▊ | 778/1000 [00:05<00:01, 150.77it/s]
79%|███████▉ | 794/1000 [00:05<00:01, 150.90it/s]
81%|████████ | 810/1000 [00:05<00:01, 151.38it/s]
83%|████████▎ | 826/1000 [00:05<00:01, 150.35it/s]
84%|████████▍ | 842/1000 [00:05<00:01, 150.51it/s]
86%|████████▌ | 858/1000 [00:05<00:00, 149.24it/s]
87%|████████▋ | 874/1000 [00:05<00:00, 151.90it/s]
89%|████████▉ | 892/1000 [00:05<00:00, 159.40it/s]
91%|█████████ | 908/1000 [00:06<00:00, 156.09it/s]
92%|█████████▎| 925/1000 [00:06<00:00, 153.92it/s]
94%|█████████▍| 941/1000 [00:06<00:00, 151.58it/s]
96%|█████████▌| 957/1000 [00:06<00:00, 150.20it/s]
97%|█████████▋| 973/1000 [00:06<00:00, 145.14it/s]
99%|█████████▉| 991/1000 [00:06<00:00, 151.12it/s]
100%|██████████| 1000/1000 [00:06<00:00, 147.88it/s]
Train NPE¶
You can then train your neural posterior estimator using npe.train_torch_ss_estimator (or npe.train_torch_time_course_estimator if you have time course data).
In [11]:
Copied!
estimator, losses = npe.train_torch_ss_estimator(
features=npe_features,
targets=npe_targets,
epochs=1000,
)
ax = losses.plot(figsize=(4, 2.5))
ax.set(xlabel="epoch", ylabel="loss")
ax.set_ylim(0, None)
plt.show()
estimator, losses = npe.train_torch_ss_estimator(
features=npe_features,
targets=npe_targets,
epochs=1000,
)
ax = losses.plot(figsize=(4, 2.5))
ax.set(xlabel="epoch", ylabel="loss")
ax.set_ylim(0, None)
plt.show()
0%| | 0/1000 [00:00<?, ?it/s]
14%|█▎ | 135/1000 [00:00<00:00, 1340.78it/s]
27%|██▋ | 270/1000 [00:00<00:00, 1336.94it/s]
41%|████ | 407/1000 [00:00<00:00, 1349.96it/s]
55%|█████▌ | 550/1000 [00:00<00:00, 1377.75it/s]
69%|██████▉ | 691/1000 [00:00<00:00, 1387.32it/s]
83%|████████▎ | 830/1000 [00:00<00:00, 1383.86it/s]
97%|█████████▋| 969/1000 [00:00<00:00, 1380.25it/s]
100%|██████████| 1000/1000 [00:00<00:00, 1372.88it/s]
Sanity check: do prior and posterior match?¶
In [12]:
Copied!
fig, (ax1, ax2) = plot.two_axes(figsize=(6, 2))
ax = sns.kdeplot(npe_targets, fill=True, ax=ax1)
ax.set_title("Prior")
posterior = estimator.predict(npe_features)
ax = sns.kdeplot(posterior, fill=True, ax=ax2)
ax.set_title("Posterior")
plt.show()
fig, (ax1, ax2) = plot.two_axes(figsize=(6, 2))
ax = sns.kdeplot(npe_targets, fill=True, ax=ax1)
ax.set_title("Prior")
posterior = estimator.predict(npe_features)
ax = sns.kdeplot(posterior, fill=True, ax=ax2)
ax.set_title("Posterior")
plt.show()
First finish line
With that you now know most of what you will need from a day-to-day basis about labelled models in modelbase2.Congratulations!
Customizing training¶
In [13]:
Copied!
from typing import TYPE_CHECKING
from modelbase2 import LinearLabelMapper, Simulator
from modelbase2.distributions import sample
from modelbase2.fns import michaelis_menten_1s
from modelbase2.parallel import parallelise
if TYPE_CHECKING:
from modelbase2.npe import AbstractEstimator
# FIXME: todo
# Show how to change Adam settings or user other optimizers
# Show how to change the surrogate network
from typing import TYPE_CHECKING
from modelbase2 import LinearLabelMapper, Simulator
from modelbase2.distributions import sample
from modelbase2.fns import michaelis_menten_1s
from modelbase2.parallel import parallelise
if TYPE_CHECKING:
from modelbase2.npe import AbstractEstimator
# FIXME: todo
# Show how to change Adam settings or user other optimizers
# Show how to change the surrogate network
Label NPE¶
In [14]:
Copied!
def get_closed_cycle() -> tuple[Model, dict[str, int], dict[str, list[int]]]:
"""
| Reaction | Labelmap |
| -------------- | -------- |
| x1 ->[v1] x2 | [0, 1] |
| x2 ->[v2a] x3 | [0, 1] |
| x2 ->[v2b] x3 | [1, 0] |
| x3 ->[v3] x1 | [0, 1] |
"""
model = (
Model()
.add_parameters(
{
"vmax_1": 1.0,
"km_1": 0.5,
"vmax_2a": 1.0,
"vmax_2b": 1.0,
"km_2": 0.5,
"vmax_3": 1.0,
"km_3": 0.5,
}
)
.add_variables({"x1": 1.0, "x2": 0.0, "x3": 0.0})
.add_reaction(
"v1",
michaelis_menten_1s,
stoichiometry={"x1": -1, "x2": 1},
args=["x1", "vmax_1", "km_1"],
)
.add_reaction(
"v2a",
michaelis_menten_1s,
stoichiometry={"x2": -1, "x3": 1},
args=["x2", "vmax_2a", "km_2"],
)
.add_reaction(
"v2b",
michaelis_menten_1s,
stoichiometry={"x2": -1, "x3": 1},
args=["x2", "vmax_2b", "km_2"],
)
.add_reaction(
"v3",
michaelis_menten_1s,
stoichiometry={"x3": -1, "x1": 1},
args=["x3", "vmax_3", "km_3"],
)
)
label_variables: dict[str, int] = {"x1": 2, "x2": 2, "x3": 2}
label_maps: dict[str, list[int]] = {
"v1": [0, 1],
"v2a": [0, 1],
"v2b": [1, 0],
"v3": [0, 1],
}
return model, label_variables, label_maps
def get_closed_cycle() -> tuple[Model, dict[str, int], dict[str, list[int]]]:
"""
| Reaction | Labelmap |
| -------------- | -------- |
| x1 ->[v1] x2 | [0, 1] |
| x2 ->[v2a] x3 | [0, 1] |
| x2 ->[v2b] x3 | [1, 0] |
| x3 ->[v3] x1 | [0, 1] |
"""
model = (
Model()
.add_parameters(
{
"vmax_1": 1.0,
"km_1": 0.5,
"vmax_2a": 1.0,
"vmax_2b": 1.0,
"km_2": 0.5,
"vmax_3": 1.0,
"km_3": 0.5,
}
)
.add_variables({"x1": 1.0, "x2": 0.0, "x3": 0.0})
.add_reaction(
"v1",
michaelis_menten_1s,
stoichiometry={"x1": -1, "x2": 1},
args=["x1", "vmax_1", "km_1"],
)
.add_reaction(
"v2a",
michaelis_menten_1s,
stoichiometry={"x2": -1, "x3": 1},
args=["x2", "vmax_2a", "km_2"],
)
.add_reaction(
"v2b",
michaelis_menten_1s,
stoichiometry={"x2": -1, "x3": 1},
args=["x2", "vmax_2b", "km_2"],
)
.add_reaction(
"v3",
michaelis_menten_1s,
stoichiometry={"x3": -1, "x1": 1},
args=["x3", "vmax_3", "km_3"],
)
)
label_variables: dict[str, int] = {"x1": 2, "x2": 2, "x3": 2}
label_maps: dict[str, list[int]] = {
"v1": [0, 1],
"v2a": [0, 1],
"v2b": [1, 0],
"v3": [0, 1],
}
return model, label_variables, label_maps
In [15]:
Copied!
def _worker(
x: tuple[tuple[int, pd.Series], tuple[int, pd.Series]],
mapper: LinearLabelMapper,
time: float,
initial_labels: dict[str, int | list[int]],
) -> pd.Series:
(_, y_ss), (_, v_ss) = x
return unwrap(
Simulator(mapper.build_model(y_ss, v_ss, initial_labels=initial_labels))
.simulate(time)
.get_concs()
).iloc[-1]
def get_label_distribution_at_time(
model: Model,
label_variables: dict[str, int],
label_maps: dict[str, list[int]],
time: float,
initial_labels: dict[str, int | list[int]],
ss_concs: pd.DataFrame,
ss_fluxes: pd.DataFrame,
) -> pd.DataFrame:
mapper = LinearLabelMapper(
model,
label_variables=label_variables,
label_maps=label_maps,
)
return pd.DataFrame(
parallelise(
partial(_worker, mapper=mapper, time=time, initial_labels=initial_labels),
inputs=list(
enumerate(zip(ss_concs.iterrows(), ss_fluxes.iterrows(), strict=True))
),
cache=None,
)
).T
def inverse_parameter_elasticity(
estimator: AbstractEstimator,
datum: pd.Series,
*,
normalized: bool = True,
displacement: float = 1e-4,
) -> pd.DataFrame:
ref = estimator.predict(datum).iloc[0, :]
coefs = {}
for name, value in datum.items():
up = coefs[name] = estimator.predict(
pd.Series(datum.to_dict() | {name: value * 1 + displacement})
).iloc[0, :]
down = coefs[name] = estimator.predict(
pd.Series(datum.to_dict() | {name: value * 1 - displacement})
).iloc[0, :]
coefs[name] = (up - down) / (2 * displacement * value)
coefs = pd.DataFrame(coefs)
if normalized:
coefs *= datum / ref.to_numpy()
return coefs
def _worker(
x: tuple[tuple[int, pd.Series], tuple[int, pd.Series]],
mapper: LinearLabelMapper,
time: float,
initial_labels: dict[str, int | list[int]],
) -> pd.Series:
(_, y_ss), (_, v_ss) = x
return unwrap(
Simulator(mapper.build_model(y_ss, v_ss, initial_labels=initial_labels))
.simulate(time)
.get_concs()
).iloc[-1]
def get_label_distribution_at_time(
model: Model,
label_variables: dict[str, int],
label_maps: dict[str, list[int]],
time: float,
initial_labels: dict[str, int | list[int]],
ss_concs: pd.DataFrame,
ss_fluxes: pd.DataFrame,
) -> pd.DataFrame:
mapper = LinearLabelMapper(
model,
label_variables=label_variables,
label_maps=label_maps,
)
return pd.DataFrame(
parallelise(
partial(_worker, mapper=mapper, time=time, initial_labels=initial_labels),
inputs=list(
enumerate(zip(ss_concs.iterrows(), ss_fluxes.iterrows(), strict=True))
),
cache=None,
)
).T
def inverse_parameter_elasticity(
estimator: AbstractEstimator,
datum: pd.Series,
*,
normalized: bool = True,
displacement: float = 1e-4,
) -> pd.DataFrame:
ref = estimator.predict(datum).iloc[0, :]
coefs = {}
for name, value in datum.items():
up = coefs[name] = estimator.predict(
pd.Series(datum.to_dict() | {name: value * 1 + displacement})
).iloc[0, :]
down = coefs[name] = estimator.predict(
pd.Series(datum.to_dict() | {name: value * 1 - displacement})
).iloc[0, :]
coefs[name] = (up - down) / (2 * displacement * value)
coefs = pd.DataFrame(coefs)
if normalized:
coefs *= datum / ref.to_numpy()
return coefs
In [16]:
Copied!
model, label_variables, label_maps = get_closed_cycle()
ss_concs, ss_fluxes = unwrap2(
Simulator(model)
.update_parameters({"vmax_2a": 1.0, "vmax_2b": 0.5})
.simulate_to_steady_state()
.get_full_concs_and_fluxes()
)
mapper = LinearLabelMapper(
model,
label_variables=label_variables,
label_maps=label_maps,
)
_, axs = plot.relative_label_distribution(
mapper,
unwrap(
Simulator(
mapper.build_model(
ss_concs.iloc[-1], ss_fluxes.iloc[-1], initial_labels={"x1": 0}
)
)
.simulate(5)
.get_concs()
),
sharey=True,
n_cols=3,
)
axs[0].set_ylabel("Relative label distribution")
axs[1].set_xlabel("Time / s")
plt.show()
model, label_variables, label_maps = get_closed_cycle()
ss_concs, ss_fluxes = unwrap2(
Simulator(model)
.update_parameters({"vmax_2a": 1.0, "vmax_2b": 0.5})
.simulate_to_steady_state()
.get_full_concs_and_fluxes()
)
mapper = LinearLabelMapper(
model,
label_variables=label_variables,
label_maps=label_maps,
)
_, axs = plot.relative_label_distribution(
mapper,
unwrap(
Simulator(
mapper.build_model(
ss_concs.iloc[-1], ss_fluxes.iloc[-1], initial_labels={"x1": 0}
)
)
.simulate(5)
.get_concs()
),
sharey=True,
n_cols=3,
)
axs[0].set_ylabel("Relative label distribution")
axs[1].set_xlabel("Time / s")
plt.show()
In [17]:
Copied!
surrogate_targets = sample(
{
"vmax_2b": Normal(0.5, 0.1),
},
n=1000,
).clip(lower=0)
ax = sns.kdeplot(surrogate_targets, fill=True)
ax.set_title("Prior")
surrogate_targets = sample(
{
"vmax_2b": Normal(0.5, 0.1),
},
n=1000,
).clip(lower=0)
ax = sns.kdeplot(surrogate_targets, fill=True)
ax.set_title("Prior")
Out[17]:
Text(0.5, 1.0, 'Prior')
In [18]:
Copied!
ss_concs, ss_fluxes = scan.steady_state(model, parameters=surrogate_targets)
ss_concs, ss_fluxes = scan.steady_state(model, parameters=surrogate_targets)
0%| | 0/1000 [00:00<?, ?it/s]
0%| | 2/1000 [00:00<00:51, 19.52it/s]
1%| | 12/1000 [00:00<00:14, 65.93it/s]
2%|▏ | 21/1000 [00:00<00:14, 66.92it/s]
3%|▎ | 29/1000 [00:00<00:13, 71.62it/s]
4%|▎ | 37/1000 [00:00<00:12, 74.42it/s]
5%|▍ | 48/1000 [00:00<00:11, 85.37it/s]
6%|▌ | 57/1000 [00:00<00:11, 80.09it/s]
7%|▋ | 67/1000 [00:00<00:10, 84.99it/s]
8%|▊ | 76/1000 [00:00<00:11, 83.59it/s]
8%|▊ | 85/1000 [00:01<00:10, 83.78it/s]
9%|▉ | 94/1000 [00:01<00:10, 83.44it/s]
10%|█ | 104/1000 [00:01<00:10, 83.62it/s]
11%|█▏ | 113/1000 [00:01<00:10, 83.62it/s]
12%|█▏ | 122/1000 [00:01<00:10, 82.69it/s]
13%|█▎ | 131/1000 [00:01<00:10, 83.61it/s]
14%|█▍ | 140/1000 [00:01<00:10, 81.27it/s]
15%|█▍ | 149/1000 [00:01<00:10, 80.03it/s]
16%|█▌ | 158/1000 [00:01<00:10, 79.63it/s]
17%|█▋ | 167/1000 [00:02<00:10, 79.90it/s]
18%|█▊ | 176/1000 [00:02<00:10, 81.39it/s]
18%|█▊ | 185/1000 [00:02<00:10, 79.23it/s]
19%|█▉ | 194/1000 [00:02<00:10, 77.88it/s]
20%|██ | 202/1000 [00:02<00:10, 78.04it/s]
21%|██ | 211/1000 [00:02<00:09, 80.91it/s]
22%|██▏ | 220/1000 [00:02<00:09, 80.90it/s]
23%|██▎ | 229/1000 [00:02<00:09, 81.63it/s]
24%|██▍ | 238/1000 [00:02<00:09, 79.58it/s]
25%|██▍ | 247/1000 [00:03<00:09, 79.91it/s]
26%|██▌ | 256/1000 [00:03<00:09, 80.86it/s]
26%|██▋ | 265/1000 [00:03<00:08, 83.10it/s]
27%|██▋ | 274/1000 [00:03<00:08, 83.88it/s]
28%|██▊ | 283/1000 [00:03<00:08, 82.11it/s]
29%|██▉ | 292/1000 [00:03<00:08, 82.80it/s]
30%|███ | 302/1000 [00:03<00:08, 84.02it/s]
31%|███ | 311/1000 [00:03<00:08, 81.34it/s]
32%|███▏ | 320/1000 [00:03<00:08, 82.24it/s]
33%|███▎ | 329/1000 [00:04<00:08, 75.72it/s]
34%|███▍ | 339/1000 [00:04<00:08, 78.49it/s]
35%|███▍ | 348/1000 [00:04<00:08, 77.82it/s]
36%|███▌ | 357/1000 [00:04<00:07, 80.40it/s]
37%|███▋ | 366/1000 [00:04<00:07, 80.37it/s]
38%|███▊ | 375/1000 [00:04<00:07, 80.38it/s]
38%|███▊ | 384/1000 [00:04<00:07, 80.64it/s]
39%|███▉ | 393/1000 [00:04<00:07, 82.39it/s]
40%|████ | 402/1000 [00:05<00:07, 81.00it/s]
41%|████ | 411/1000 [00:05<00:07, 82.57it/s]
42%|████▏ | 420/1000 [00:05<00:07, 80.92it/s]
43%|████▎ | 429/1000 [00:05<00:07, 80.39it/s]
44%|████▍ | 438/1000 [00:05<00:06, 81.33it/s]
45%|████▍ | 448/1000 [00:05<00:06, 82.75it/s]
46%|████▌ | 457/1000 [00:05<00:06, 80.98it/s]
47%|████▋ | 466/1000 [00:05<00:06, 83.34it/s]
48%|████▊ | 476/1000 [00:05<00:06, 81.04it/s]
48%|████▊ | 485/1000 [00:06<00:06, 80.79it/s]
50%|████▉ | 496/1000 [00:06<00:06, 82.56it/s]
50%|█████ | 505/1000 [00:06<00:06, 79.70it/s]
52%|█████▏ | 516/1000 [00:06<00:05, 83.91it/s]
52%|█████▎ | 525/1000 [00:06<00:05, 83.98it/s]
53%|█████▎ | 534/1000 [00:06<00:05, 82.18it/s]
54%|█████▍ | 544/1000 [00:06<00:05, 82.59it/s]
55%|█████▌ | 554/1000 [00:06<00:05, 84.41it/s]
56%|█████▋ | 563/1000 [00:06<00:05, 84.83it/s]
57%|█████▋ | 572/1000 [00:07<00:05, 84.19it/s]
58%|█████▊ | 581/1000 [00:07<00:05, 83.39it/s]
59%|█████▉ | 590/1000 [00:07<00:05, 76.06it/s]
60%|██████ | 600/1000 [00:07<00:04, 81.30it/s]
61%|██████ | 609/1000 [00:07<00:04, 82.70it/s]
62%|██████▏ | 618/1000 [00:07<00:04, 80.05it/s]
63%|██████▎ | 627/1000 [00:07<00:04, 80.99it/s]
64%|██████▎ | 636/1000 [00:07<00:04, 79.72it/s]
64%|██████▍ | 645/1000 [00:07<00:04, 80.74it/s]
65%|██████▌ | 654/1000 [00:08<00:04, 79.67it/s]
66%|██████▌ | 662/1000 [00:08<00:04, 79.53it/s]
67%|██████▋ | 670/1000 [00:08<00:04, 79.35it/s]
68%|██████▊ | 678/1000 [00:08<00:04, 77.73it/s]
69%|██████▊ | 686/1000 [00:08<00:04, 78.03it/s]
70%|██████▉ | 695/1000 [00:08<00:03, 80.24it/s]
70%|███████ | 704/1000 [00:08<00:03, 77.49it/s]
71%|███████▏ | 713/1000 [00:08<00:03, 79.85it/s]
72%|███████▏ | 723/1000 [00:08<00:03, 81.76it/s]
73%|███████▎ | 732/1000 [00:09<00:03, 79.06it/s]
74%|███████▍ | 742/1000 [00:09<00:03, 83.15it/s]
75%|███████▌ | 751/1000 [00:09<00:03, 82.88it/s]
76%|███████▌ | 760/1000 [00:09<00:02, 82.36it/s]
77%|███████▋ | 769/1000 [00:09<00:03, 76.00it/s]
78%|███████▊ | 779/1000 [00:09<00:02, 81.07it/s]
79%|███████▉ | 788/1000 [00:09<00:02, 82.37it/s]
80%|███████▉ | 797/1000 [00:09<00:02, 78.01it/s]
81%|████████ | 806/1000 [00:09<00:02, 81.11it/s]
82%|████████▏ | 815/1000 [00:10<00:02, 80.62it/s]
82%|████████▏ | 824/1000 [00:10<00:02, 82.87it/s]
83%|████████▎ | 833/1000 [00:10<00:02, 78.72it/s]
84%|████████▍ | 842/1000 [00:10<00:01, 81.09it/s]
85%|████████▌ | 851/1000 [00:10<00:01, 80.35it/s]
86%|████████▌ | 860/1000 [00:10<00:01, 77.44it/s]
87%|████████▋ | 869/1000 [00:10<00:01, 79.57it/s]
88%|████████▊ | 879/1000 [00:10<00:01, 84.55it/s]
89%|████████▉ | 888/1000 [00:11<00:01, 80.74it/s]
90%|████████▉ | 897/1000 [00:11<00:01, 80.77it/s]
91%|█████████ | 908/1000 [00:11<00:01, 83.24it/s]
92%|█████████▏| 917/1000 [00:11<00:00, 83.42it/s]
93%|█████████▎| 926/1000 [00:11<00:00, 84.92it/s]
94%|█████████▎| 935/1000 [00:11<00:00, 83.48it/s]
94%|█████████▍| 944/1000 [00:11<00:00, 77.16it/s]
95%|█████████▌| 954/1000 [00:11<00:00, 82.81it/s]
96%|█████████▋| 963/1000 [00:11<00:00, 81.13it/s]
97%|█████████▋| 972/1000 [00:12<00:00, 81.83it/s]
98%|█████████▊| 981/1000 [00:12<00:00, 83.46it/s]
99%|█████████▉| 991/1000 [00:12<00:00, 85.62it/s]
100%|██████████| 1000/1000 [00:12<00:00, 86.12it/s]
100%|██████████| 1000/1000 [00:12<00:00, 80.86it/s]
In [19]:
Copied!
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
_, ax = plot.violins(ss_concs, ax=ax1)
ax.set_ylabel("Concentration / a.u.")
_, ax = plot.violins(ss_fluxes, ax=ax2)
ax.set_ylabel("Flux / a.u.")
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
_, ax = plot.violins(ss_concs, ax=ax1)
ax.set_ylabel("Concentration / a.u.")
_, ax = plot.violins(ss_fluxes, ax=ax2)
ax.set_ylabel("Flux / a.u.")
Out[19]:
Text(0, 0.5, 'Flux / a.u.')
In [20]:
Copied!
surrogate_features = get_label_distribution_at_time(
model=model,
label_variables=label_variables,
label_maps=label_maps,
time=5,
ss_concs=ss_concs,
ss_fluxes=ss_fluxes,
initial_labels={"x1": 0},
)
_, ax = plot.violins(surrogate_features)
ax.set_ylabel("Relative label distribution")
surrogate_features = get_label_distribution_at_time(
model=model,
label_variables=label_variables,
label_maps=label_maps,
time=5,
ss_concs=ss_concs,
ss_fluxes=ss_fluxes,
initial_labels={"x1": 0},
)
_, ax = plot.violins(surrogate_features)
ax.set_ylabel("Relative label distribution")
0%| | 0/1000 [00:00<?, ?it/s]
0%| | 1/1000 [00:00<01:42, 9.71it/s]
1%| | 9/1000 [00:00<00:20, 49.37it/s]
2%|▏ | 17/1000 [00:00<00:15, 61.85it/s]
2%|▎ | 25/1000 [00:00<00:14, 67.27it/s]
3%|▎ | 33/1000 [00:00<00:13, 70.18it/s]
4%|▍ | 41/1000 [00:00<00:13, 72.18it/s]
5%|▍ | 49/1000 [00:00<00:13, 72.66it/s]
6%|▌ | 57/1000 [00:00<00:12, 73.09it/s]
6%|▋ | 65/1000 [00:00<00:12, 74.49it/s]
7%|▋ | 73/1000 [00:01<00:13, 70.90it/s]
8%|▊ | 84/1000 [00:01<00:11, 80.78it/s]
9%|▉ | 93/1000 [00:01<00:12, 74.93it/s]
10%|█ | 101/1000 [00:01<00:11, 75.44it/s]
11%|█ | 109/1000 [00:01<00:11, 76.35it/s]
12%|█▏ | 117/1000 [00:01<00:11, 76.90it/s]
12%|█▎ | 125/1000 [00:01<00:11, 75.15it/s]
13%|█▎ | 133/1000 [00:01<00:11, 76.05it/s]
14%|█▍ | 141/1000 [00:01<00:11, 74.47it/s]
15%|█▍ | 149/1000 [00:02<00:11, 74.29it/s]
16%|█▌ | 157/1000 [00:02<00:11, 74.04it/s]
16%|█▋ | 165/1000 [00:02<00:11, 74.88it/s]
17%|█▋ | 173/1000 [00:02<00:10, 75.78it/s]
18%|█▊ | 181/1000 [00:02<00:10, 76.67it/s]
19%|█▉ | 189/1000 [00:02<00:10, 76.17it/s]
20%|█▉ | 197/1000 [00:02<00:10, 76.71it/s]
20%|██ | 205/1000 [00:02<00:10, 77.35it/s]
21%|██▏ | 213/1000 [00:02<00:10, 75.63it/s]
22%|██▏ | 222/1000 [00:03<00:09, 79.63it/s]
23%|██▎ | 230/1000 [00:03<00:09, 78.20it/s]
24%|██▍ | 238/1000 [00:03<00:09, 77.34it/s]
25%|██▍ | 246/1000 [00:03<00:09, 77.46it/s]
25%|██▌ | 254/1000 [00:03<00:09, 77.34it/s]
26%|██▌ | 262/1000 [00:03<00:09, 77.40it/s]
27%|██▋ | 270/1000 [00:03<00:09, 76.80it/s]
28%|██▊ | 278/1000 [00:03<00:09, 74.14it/s]
29%|██▊ | 286/1000 [00:03<00:09, 74.14it/s]
29%|██▉ | 294/1000 [00:03<00:09, 74.98it/s]
30%|███ | 302/1000 [00:04<00:09, 75.22it/s]
31%|███ | 310/1000 [00:04<00:09, 73.86it/s]
32%|███▏ | 318/1000 [00:04<00:09, 73.96it/s]
33%|███▎ | 326/1000 [00:04<00:08, 74.93it/s]
33%|███▎ | 334/1000 [00:04<00:08, 74.67it/s]
34%|███▍ | 342/1000 [00:04<00:08, 74.23it/s]
35%|███▌ | 350/1000 [00:04<00:08, 73.85it/s]
36%|███▌ | 358/1000 [00:04<00:08, 74.57it/s]
37%|███▋ | 366/1000 [00:04<00:08, 74.04it/s]
37%|███▋ | 374/1000 [00:05<00:08, 75.03it/s]
38%|███▊ | 382/1000 [00:05<00:08, 76.32it/s]
39%|███▉ | 390/1000 [00:05<00:07, 76.62it/s]
40%|███▉ | 398/1000 [00:05<00:07, 75.81it/s]
41%|████ | 406/1000 [00:05<00:07, 75.83it/s]
41%|████▏ | 414/1000 [00:05<00:07, 75.66it/s]
42%|████▏ | 422/1000 [00:05<00:07, 75.15it/s]
43%|████▎ | 430/1000 [00:05<00:07, 74.56it/s]
44%|████▍ | 438/1000 [00:05<00:07, 75.86it/s]
45%|████▍ | 446/1000 [00:05<00:07, 75.27it/s]
45%|████▌ | 454/1000 [00:06<00:07, 75.59it/s]
46%|████▌ | 462/1000 [00:06<00:07, 74.84it/s]
47%|████▋ | 470/1000 [00:06<00:07, 75.17it/s]
48%|████▊ | 478/1000 [00:06<00:06, 75.33it/s]
49%|████▊ | 486/1000 [00:06<00:06, 74.23it/s]
49%|████▉ | 494/1000 [00:06<00:06, 72.74it/s]
50%|█████ | 502/1000 [00:06<00:06, 73.90it/s]
51%|█████ | 510/1000 [00:06<00:06, 73.51it/s]
52%|█████▏ | 518/1000 [00:06<00:06, 73.08it/s]
53%|█████▎ | 526/1000 [00:07<00:06, 72.61it/s]
53%|█████▎ | 534/1000 [00:07<00:06, 72.54it/s]
54%|█████▍ | 542/1000 [00:07<00:06, 72.30it/s]
55%|█████▌ | 550/1000 [00:07<00:06, 72.00it/s]
56%|█████▌ | 558/1000 [00:07<00:05, 73.88it/s]
57%|█████▋ | 566/1000 [00:07<00:05, 75.15it/s]
57%|█████▋ | 574/1000 [00:07<00:05, 75.49it/s]
58%|█████▊ | 582/1000 [00:07<00:05, 75.13it/s]
59%|█████▉ | 590/1000 [00:07<00:05, 75.64it/s]
60%|█████▉ | 598/1000 [00:08<00:05, 75.45it/s]
61%|██████ | 606/1000 [00:08<00:05, 74.59it/s]
61%|██████▏ | 614/1000 [00:08<00:05, 75.33it/s]
62%|██████▏ | 622/1000 [00:08<00:04, 76.06it/s]
63%|██████▎ | 630/1000 [00:08<00:04, 75.19it/s]
64%|██████▍ | 638/1000 [00:08<00:04, 76.00it/s]
65%|██████▍ | 646/1000 [00:08<00:04, 76.62it/s]
65%|██████▌ | 654/1000 [00:08<00:04, 76.79it/s]
66%|██████▌ | 662/1000 [00:08<00:04, 76.92it/s]
67%|██████▋ | 670/1000 [00:08<00:04, 75.83it/s]
68%|██████▊ | 678/1000 [00:09<00:04, 75.10it/s]
69%|██████▊ | 686/1000 [00:09<00:04, 76.14it/s]
69%|██████▉ | 694/1000 [00:09<00:03, 76.79it/s]
70%|███████ | 702/1000 [00:09<00:04, 72.45it/s]
71%|███████ | 710/1000 [00:09<00:03, 74.33it/s]
72%|███████▏ | 718/1000 [00:09<00:03, 75.61it/s]
73%|███████▎ | 726/1000 [00:09<00:03, 75.73it/s]
73%|███████▎ | 734/1000 [00:09<00:03, 76.57it/s]
74%|███████▍ | 742/1000 [00:09<00:03, 75.31it/s]
75%|███████▌ | 750/1000 [00:10<00:03, 76.50it/s]
76%|███████▌ | 758/1000 [00:10<00:03, 75.71it/s]
77%|███████▋ | 766/1000 [00:10<00:03, 76.36it/s]
77%|███████▋ | 774/1000 [00:10<00:02, 75.35it/s]
78%|███████▊ | 783/1000 [00:10<00:02, 76.02it/s]
79%|███████▉ | 791/1000 [00:10<00:02, 75.36it/s]
80%|███████▉ | 799/1000 [00:10<00:02, 75.74it/s]
81%|████████ | 807/1000 [00:10<00:02, 74.95it/s]
82%|████████▏ | 815/1000 [00:10<00:02, 75.21it/s]
82%|████████▏ | 823/1000 [00:11<00:02, 74.66it/s]
83%|████████▎ | 831/1000 [00:11<00:02, 74.52it/s]
84%|████████▍ | 839/1000 [00:11<00:02, 74.19it/s]
85%|████████▍ | 847/1000 [00:11<00:02, 75.04it/s]
86%|████████▌ | 855/1000 [00:11<00:01, 75.84it/s]
86%|████████▋ | 863/1000 [00:11<00:01, 70.19it/s]
87%|████████▋ | 872/1000 [00:11<00:01, 74.30it/s]
88%|████████▊ | 880/1000 [00:11<00:01, 75.65it/s]
89%|████████▉ | 888/1000 [00:11<00:01, 76.32it/s]
90%|████████▉ | 896/1000 [00:11<00:01, 76.20it/s]
90%|█████████ | 904/1000 [00:12<00:01, 75.82it/s]
91%|█████████ | 912/1000 [00:12<00:01, 75.20it/s]
92%|█████████▏| 920/1000 [00:12<00:01, 76.08it/s]
93%|█████████▎| 928/1000 [00:12<00:00, 75.85it/s]
94%|█████████▎| 936/1000 [00:12<00:00, 75.37it/s]
94%|█████████▍| 944/1000 [00:12<00:00, 75.07it/s]
95%|█████████▌| 952/1000 [00:12<00:00, 73.55it/s]
96%|█████████▌| 960/1000 [00:12<00:00, 73.75it/s]
97%|█████████▋| 968/1000 [00:12<00:00, 74.71it/s]
98%|█████████▊| 976/1000 [00:13<00:00, 74.48it/s]
98%|█████████▊| 984/1000 [00:13<00:00, 74.95it/s]
99%|█████████▉| 992/1000 [00:13<00:00, 75.58it/s]
100%|██████████| 1000/1000 [00:13<00:00, 74.20it/s]
Out[20]:
Text(0, 0.5, 'Relative label distribution')
In [21]:
Copied!
estimator, losses = npe.train_torch_ss_estimator(
features=surrogate_features,
targets=surrogate_targets,
epochs=2_000,
)
ax = losses.plot()
ax.set_ylim(0, None)
estimator, losses = npe.train_torch_ss_estimator(
features=surrogate_features,
targets=surrogate_targets,
epochs=2_000,
)
ax = losses.plot()
ax.set_ylim(0, None)
0%| | 0/2000 [00:00<?, ?it/s]
7%|▋ | 144/2000 [00:00<00:01, 1431.83it/s]
14%|█▍ | 288/2000 [00:00<00:01, 1417.93it/s]
22%|██▏ | 436/2000 [00:00<00:01, 1445.63it/s]
29%|██▉ | 586/2000 [00:00<00:00, 1466.61it/s]
37%|███▋ | 737/2000 [00:00<00:00, 1479.53it/s]
44%|████▍ | 887/2000 [00:00<00:00, 1485.49it/s]
52%|█████▏ | 1036/2000 [00:00<00:00, 1486.83it/s]
59%|█████▉ | 1186/2000 [00:00<00:00, 1489.61it/s]
67%|██████▋ | 1335/2000 [00:00<00:00, 1474.31it/s]
74%|███████▍ | 1483/2000 [00:01<00:00, 1457.94it/s]
82%|████████▏ | 1633/2000 [00:01<00:00, 1468.69it/s]
89%|████████▉ | 1780/2000 [00:01<00:00, 1454.42it/s]
96%|█████████▋| 1927/2000 [00:01<00:00, 1457.00it/s]
100%|██████████| 2000/2000 [00:01<00:00, 1463.98it/s]
Out[21]:
(0.0, 0.5189851683098823)
In [22]:
Copied!
fig, (ax1, ax2) = plt.subplots(
1,
2,
figsize=(8, 3),
layout="constrained",
sharex=True,
sharey=False,
)
ax = sns.kdeplot(surrogate_targets, fill=True, ax=ax1)
ax.set_title("Prior")
posterior = estimator.predict(surrogate_features)
ax = sns.kdeplot(posterior, fill=True, ax=ax2)
ax.set_title("Posterior")
ax2.set_ylim(*ax1.get_ylim())
plt.show()
fig, (ax1, ax2) = plt.subplots(
1,
2,
figsize=(8, 3),
layout="constrained",
sharex=True,
sharey=False,
)
ax = sns.kdeplot(surrogate_targets, fill=True, ax=ax1)
ax.set_title("Prior")
posterior = estimator.predict(surrogate_features)
ax = sns.kdeplot(posterior, fill=True, ax=ax2)
ax.set_title("Posterior")
ax2.set_ylim(*ax1.get_ylim())
plt.show()
Inverse parameter sensitivity¶
In [23]:
Copied!
_ = plot.heatmap(inverse_parameter_elasticity(estimator, surrogate_features.iloc[0]))
_ = plot.heatmap(inverse_parameter_elasticity(estimator, surrogate_features.iloc[0]))
In [24]:
Copied!
elasticities = pd.DataFrame(
{
k: inverse_parameter_elasticity(estimator, i).loc["vmax_2b"]
for k, i in surrogate_features.iterrows()
}
).T
_ = plot.violins(elasticities)
elasticities = pd.DataFrame(
{
k: inverse_parameter_elasticity(estimator, i).loc["vmax_2b"]
for k, i in surrogate_features.iterrows()
}
).T
_ = plot.violins(elasticities)
In [ ]:
Copied!