In [1]:

from pathlib import Path

import matplotlib.pyplot as plt

from modelbase2 import Model, fns, mc, plot
from modelbase2.distributions import GaussianKde, sample
from modelbase2.parameterise import get_km_and_kcat_from_brenda

from pathlib import Path import matplotlib.pyplot as plt from modelbase2 import Model, fns, mc, plot from modelbase2.distributions import GaussianKde, sample from modelbase2.parameterise import get_km_and_kcat_from_brenda

Model parameterisation¶

Obtaining experimentally measured parameters can be challenging.

Using the Brenda enzymes database we can obtain distributions of enzymatic parameters for a wide range of organisms.

We can do that with the modelbase2.parameterise module.

These distributions can then in turn be used with our Monte-Carlo methods to capture the range of possible behaviour your model can exhibit.

+ =

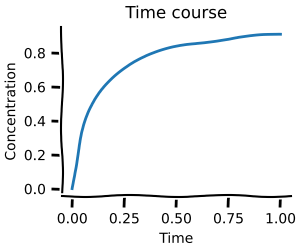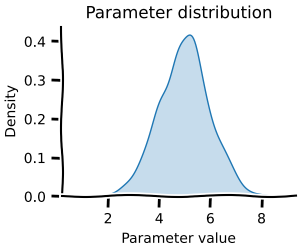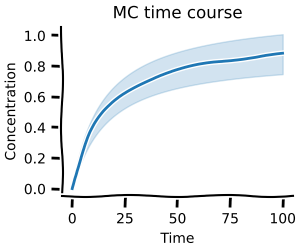
In order to obtain the parameters for a given Enzyme commision number (ec) we will manually download the database.
You have to do this manually due to the brenda licensing terms.

Note: we have created a small copy of just the rubisco data here to keep the documentation running.
Adjust your brenda_path accordingly

In [2]:

kms, kcats = get_km_and_kcat_from_brenda(
    ec="4.1.1.39",
    brenda_path=Path("assets") / "brenda_rubisco_only.json",
)

print(f"Found: {len(kms)} michaelis constants")
kms.head()

kms, kcats = get_km_and_kcat_from_brenda( ec="4.1.1.39", brenda_path=Path("assets") / "brenda_rubisco_only.json", ) print(f"Found: {len(kms)} michaelis constants") kms.head()

Found: 668 michaelis constants

Out[2]:

	value	substrate	organism	uniprot	sequence
0	0.0290	CO2	Amphicarpaea bracteata	A0A1C3HPM0	MSPQTETKASVGFKAGVKDYKLTYYTPDYETKDTDILAAFRVTPQP...
5	0.0510	CO2	Archaeoglobus fulgidus	O28635	MAEFEIYREYVDKSYEPQKDDIVAVFRITPAEGFTIEDAAGAVAAE...
7	0.0279	CO2	Hordeum murinum	A0A1C3HPQ4	MSPQTETKAGVGFKAGVKDYKLTYYTPEYETKDTDILAAFRVSPQP...
8	0.0279	CO2	Hordeum brachyantherum	A0A1C3HPQ0	MSPQTETKAGVGFQAGVKDYKLTYYTPEYETKDTDILAAFRVSPQP...
9	0.0195	CO2	Glycine canescens	A0A1C3HPP9	MSPQTETKASVGFKAGVKDYKLTYYTPDYETKDTDILAAFRVTPQP...

As you can see above, this provides you with parameter values for different organisms and substrates.
Thus, we first filter by the specific substrate we are interested in.

In [3]:

# Filter out a specific substrate
kms = kms[kms["substrate"] == "CO2"]
kcats = kcats[kcats["substrate"] == "CO2"]

print(f"Filtered to {len(kms)} michaelis constants")
kms.head()

# Filter out a specific substrate kms = kms[kms["substrate"] == "CO2"] kcats = kcats[kcats["substrate"] == "CO2"] print(f"Filtered to {len(kms)} michaelis constants") kms.head()

Filtered to 443 michaelis constants

Out[3]:

	value	substrate	organism	uniprot	sequence
0	0.0290	CO2	Amphicarpaea bracteata	A0A1C3HPM0	MSPQTETKASVGFKAGVKDYKLTYYTPDYETKDTDILAAFRVTPQP...
5	0.0510	CO2	Archaeoglobus fulgidus	O28635	MAEFEIYREYVDKSYEPQKDDIVAVFRITPAEGFTIEDAAGAVAAE...
7	0.0279	CO2	Hordeum murinum	A0A1C3HPQ4	MSPQTETKAGVGFKAGVKDYKLTYYTPEYETKDTDILAAFRVSPQP...
8	0.0279	CO2	Hordeum brachyantherum	A0A1C3HPQ0	MSPQTETKAGVGFQAGVKDYKLTYYTPEYETKDTDILAAFRVSPQP...
9	0.0195	CO2	Glycine canescens	A0A1C3HPP9	MSPQTETKASVGFKAGVKDYKLTYYTPDYETKDTDILAAFRVTPQP...

Since these are sufficiently many values, we can create a Gaussian Kernel Density estimate of them.

In [4]:

km_dist = GaussianKde.from_data(kms["value"])
fig, ax = km_dist.plot(
    xmin=kms["value"].min() * 0.8,
    xmax=kms["value"].max() * 1.2,
)
ax.set(title=f"rubisco km for CO2, n={len(kms)}")
plt.show()

km_dist = GaussianKde.from_data(kms["value"]) fig, ax = km_dist.plot( xmin=kms["value"].min() * 0.8, xmax=kms["value"].max() * 1.2, ) ax.set(title=f"rubisco km for CO2, n={len(kms)}") plt.show()

This kernel density estimate we can now use exactly like other distribution in our Monte-Carlo routines (see the Monte Carlo notebook for more information).

Here, we create a small toy model and then use the distribution obtained from the experimental data to calculate the steady-state distribution of the model concentration.

In [5]:

model = (
    Model()
    .add_parameters({"k_out": 1.0, "km": 1.0})
    .add_variable("PGA", 0)
    .add_reaction(
        "rubisco",
        fns.constant,
        args=["km"],
        stoichiometry={"PGA": 2},
    )
    .add_reaction(
        "outflux",
        fns.mass_action_1s,
        args=["PGA", "k_out"],
        stoichiometry={"PGA": -1},
    )
)

ss = mc.steady_state(model, mc_parameters=sample({"km": km_dist}, n=10))

fig, ax = plt.subplots(figsize=(4, 3))
ax.set(ylabel="Steady-state concentration")
plot.violins(ss.concs, ax=ax)
plt.show()

model = ( Model() .add_parameters({"k_out": 1.0, "km": 1.0}) .add_variable("PGA", 0) .add_reaction( "rubisco", fns.constant, args=["km"], stoichiometry={"PGA": 2}, ) .add_reaction( "outflux", fns.mass_action_1s, args=["PGA", "k_out"], stoichiometry={"PGA": -1}, ) ) ss = mc.steady_state(model, mc_parameters=sample({"km": km_dist}, n=10)) fig, ax = plt.subplots(figsize=(4, 3)) ax.set(ylabel="Steady-state concentration") plot.violins(ss.concs, ax=ax) plt.show()

  0%|          | 0/10 [00:00<?, ?it/s]

100%|██████████| 10/10 [00:00<00:00, 69.78it/s]

First finish line

With that you now know most of what you will need from a day-to-day basis about parameter scans in modelbase2.

Congratulations!