In [1]:

from __future__ import annotations

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

import modelbase2 as mb2
from example_models import (
    get_lin_chain_two_circles,
    get_linear_chain_2v,
    get_upper_glycolysis,
)
from modelbase2 import make_protocol, mc, mca, plot

from __future__ import annotations import matplotlib.pyplot as plt import numpy as np import pandas as pd import modelbase2 as mb2 from example_models import ( get_lin_chain_two_circles, get_linear_chain_2v, get_upper_glycolysis, ) from modelbase2 import make_protocol, mc, mca, plot

Monte Carlo methods¶

Almost every parameter in biology is better described with a distribution than a single value.
Monte-carlo methods allow you to capture the range of possible behaviour your model can exhibit.
This is especially useful when you want to understand the uncertainty in your model's predictions.

modelbase2 offers these Monte Carlo methods for all scans ...

+ =

and even for metabolic control analysis

+ =

In this tutorial we will mostly use the modelbase2.distributions and modelbase2.mca modules, which contain the functionality to sample from distributions and run distributed analyses.

Sample values¶

To do any Monte-Carlo analysis, we first need to be able to sample values.

For that, you can use the sample function and distributions supplied by modelbase2.
These are mostly thin wrappers around the numpy and scipy sampling methods.

In [2]:

from modelbase2.distributions import LogNormal, Uniform, sample

sample(
    {
        "k2": Uniform(1.0, 2.0),
        "k3": LogNormal(mean=1.0, sigma=1.0),
    },
    n=5,
)

from modelbase2.distributions import LogNormal, Uniform, sample sample( { "k2": Uniform(1.0, 2.0), "k3": LogNormal(mean=1.0, sigma=1.0), }, n=5, )

Out[2]:

	k2	k3
0	1.773956	0.739205
1	1.438878	3.088978
2	1.858598	1.981308
3	1.697368	2.672993
4	1.094177	1.158303

Steady-state¶

Using mc.steady_state you can calculate the steady-state distribution given the monte-carlo parameters.

This works analogously to the scan.steady_state function, except the index of the dataframes is always just an integer.

The parameters used can be obtained by result.parameters.

We will use a linear chain of reactions with two circles as an example model for this notebook.

$$ \begin{array}{c|c} \mathrm{Reaction} & \mathrm{Stoichiometry} \\ \hline v_0 & \varnothing \rightarrow{} \mathrm{x_1} \\ v_1 & -\mathrm{x_1} \rightarrow{} \mathrm{x_2} \\ v_2 & -\mathrm{x_1} \rightarrow{} \mathrm{x_3} \\ v_3 & -\mathrm{x_1} \rightarrow{} \mathrm{x_4} \\ v_4 & -\mathrm{x_4} \rightarrow{} \varnothing\\ v_5 & -\mathrm{x_2} \rightarrow{} \mathrm{x_1} \\ v_6 & -\mathrm{x_3} \rightarrow{} \mathrm{x_1} \\ \end{array} $$

In [3]:

ss = mc.steady_state(
    get_linear_chain_2v(),
    mc_parameters=sample(
        {
            "k1": Uniform(0.9, 1.1),
            "k2": Uniform(1.0, 1.3),
            "k3": LogNormal(mean=1.0, sigma=0.2),
        },
        n=10,
    ),
)

fig, (ax1, ax2) = plot.two_axes(figsize=(6, 2.5), sharex=False)
plot.violins(ss.concs, ax=ax1)
plot.violins(ss.fluxes, ax=ax2)
ax1.set(xlabel="Variables", ylabel="Concentration / a.u.")
ax2.set(xlabel="Reactions", ylabel="Flux / a.u.")
plt.show()

ss = mc.steady_state( get_linear_chain_2v(), mc_parameters=sample( { "k1": Uniform(0.9, 1.1), "k2": Uniform(1.0, 1.3), "k3": LogNormal(mean=1.0, sigma=0.2), }, n=10, ), ) fig, (ax1, ax2) = plot.two_axes(figsize=(6, 2.5), sharex=False) plot.violins(ss.concs, ax=ax1) plot.violins(ss.fluxes, ax=ax2) ax1.set(xlabel="Variables", ylabel="Concentration / a.u.") ax2.set(xlabel="Reactions", ylabel="Flux / a.u.") plt.show()

  0%|          | 0/10 [00:00<?, ?it/s]

 70%|███████   | 7/10 [00:00<00:00, 69.98it/s]

100%|██████████| 10/10 [00:00<00:00, 69.84it/s]

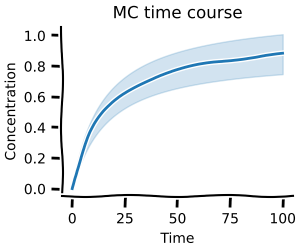
Time course¶

Using mc.time_course you can calculate time courses for sampled parameters.

+ =

This function works analogously to scan.time_course.

The pandas.DataFrames for concentrations and fluxes have a n x time pandas.MultiIndex.

The corresponding parameters can be found in result.parameters

In [4]:

tc = mc.time_course(
    get_linear_chain_2v(),
    time_points=np.linspace(0, 1, 11),
    mc_parameters=sample(
        {
            "k1": Uniform(0.9, 1.1),
            "k2": Uniform(1.0, 1.3),
            "k3": LogNormal(mean=1.0, sigma=0.2),
        },
        n=10,
    ),
)

fig, (ax1, ax2) = plot.two_axes(figsize=(7, 4))
plot.lines_mean_std_from_2d_idx(tc.concs, ax=ax1)
plot.lines_mean_std_from_2d_idx(tc.fluxes, ax=ax2)
ax1.set(xlabel="Time / a.u", ylabel="Concentration / a.u.")
ax2.set(xlabel="Time / a.u", ylabel="Flux / a.u.")
plt.show()

tc = mc.time_course( get_linear_chain_2v(), time_points=np.linspace(0, 1, 11), mc_parameters=sample( { "k1": Uniform(0.9, 1.1), "k2": Uniform(1.0, 1.3), "k3": LogNormal(mean=1.0, sigma=0.2), }, n=10, ), ) fig, (ax1, ax2) = plot.two_axes(figsize=(7, 4)) plot.lines_mean_std_from_2d_idx(tc.concs, ax=ax1) plot.lines_mean_std_from_2d_idx(tc.fluxes, ax=ax2) ax1.set(xlabel="Time / a.u", ylabel="Concentration / a.u.") ax2.set(xlabel="Time / a.u", ylabel="Flux / a.u.") plt.show()

  0%|          | 0/10 [00:00<?, ?it/s]

100%|██████████| 10/10 [00:00<00:00, 63.26it/s]

Protocol time course¶

Using mc.time_course_over_protocol you can calculate time courses for sampled parameters given a discrete protocol.

+ =

The pandas.DataFrames for concentrations and fluxes have a n x time pandas.MultiIndex.
The corresponding parameters can be found in scan.parameters

In [5]:

tc = mc.time_course_over_protocol(
    get_linear_chain_2v(),
    time_points_per_step=10,
    protocol=make_protocol(
        [
            (1, {"k1": 1}),
            (2, {"k1": 2}),
            (3, {"k1": 1}),
        ]
    ),
    mc_parameters=sample(
        {
            "k2": Uniform(1.0, 1.3),
            "k3": LogNormal(mean=1.0, sigma=0.2),
        },
        n=10,
    ),
)

fig, (ax1, ax2) = plot.two_axes(figsize=(7, 4))
plot.lines_mean_std_from_2d_idx(tc.concs, ax=ax1)
plot.lines_mean_std_from_2d_idx(tc.fluxes, ax=ax2)
for ax in (ax1, ax2):
    plot.shade_protocol(tc.protocol["k1"], ax=ax, alpha=0.1)

ax1.set(xlabel="Time / a.u", ylabel="Concentration / a.u.")
ax2.set(xlabel="Time / a.u", ylabel="Flux / a.u.")
plt.show()

tc = mc.time_course_over_protocol( get_linear_chain_2v(), time_points_per_step=10, protocol=make_protocol( [ (1, {"k1": 1}), (2, {"k1": 2}), (3, {"k1": 1}), ] ), mc_parameters=sample( { "k2": Uniform(1.0, 1.3), "k3": LogNormal(mean=1.0, sigma=0.2), }, n=10, ), ) fig, (ax1, ax2) = plot.two_axes(figsize=(7, 4)) plot.lines_mean_std_from_2d_idx(tc.concs, ax=ax1) plot.lines_mean_std_from_2d_idx(tc.fluxes, ax=ax2) for ax in (ax1, ax2): plot.shade_protocol(tc.protocol["k1"], ax=ax, alpha=0.1) ax1.set(xlabel="Time / a.u", ylabel="Concentration / a.u.") ax2.set(xlabel="Time / a.u", ylabel="Flux / a.u.") plt.show()

  0%|          | 0/10 [00:00<?, ?it/s]

 50%|█████     | 5/10 [00:00<00:00, 37.53it/s]

100%|██████████| 10/10 [00:00<00:00, 38.16it/s]

Metabolic control analysis¶

modelbase2 further has routines for monte-carlo distributed metabolic control analysis.
This allows quantifying, whether the coefficients obtained from the MCA analysis are robust against parameter changes or whether they are just an artifact of a particular choice of parameters.

Variable elasticities¶

+ =

The returned pandas.DataFrame has a pd.MultiIndex of shape n x reaction.

In [6]:

mc_elas = mc.variable_elasticities(
    get_upper_glycolysis(),
    concs={
        "GLC": 0.3,
        "G6P": 0.4,
        "F6P": 0.5,
        "FBP": 0.6,
        "ATP": 0.4,
        "ADP": 0.6,
    },
    variables=["GLC", "F6P"],
    mc_parameters=sample(
        {
            # "k1": LogNormal(mean=np.log(0.25), sigma=1.0),
            # "k2": LogNormal(mean=np.log(1.0), sigma=1.0),
            "k3": LogNormal(mean=np.log(1.0), sigma=1.0),
            # "k4": LogNormal(mean=np.log(1.0), sigma=1.0),
            # "k5": LogNormal(mean=np.log(1.0), sigma=1.0),
            # "k6": LogNormal(mean=np.log(1.0), sigma=1.0),
            # "k7": LogNormal(mean=np.log(2.5), sigma=1.0),
        },
        n=5,
    ),
)

_ = plot.violins_from_2d_idx(mc_elas)
plt.show()

mc_elas = mc.variable_elasticities( get_upper_glycolysis(), concs={ "GLC": 0.3, "G6P": 0.4, "F6P": 0.5, "FBP": 0.6, "ATP": 0.4, "ADP": 0.6, }, variables=["GLC", "F6P"], mc_parameters=sample( { # "k1": LogNormal(mean=np.log(0.25), sigma=1.0), # "k2": LogNormal(mean=np.log(1.0), sigma=1.0), "k3": LogNormal(mean=np.log(1.0), sigma=1.0), # "k4": LogNormal(mean=np.log(1.0), sigma=1.0), # "k5": LogNormal(mean=np.log(1.0), sigma=1.0), # "k6": LogNormal(mean=np.log(1.0), sigma=1.0), # "k7": LogNormal(mean=np.log(2.5), sigma=1.0), }, n=5, ), ) _ = plot.violins_from_2d_idx(mc_elas) plt.show()

  0%|          | 0/5 [00:00<?, ?it/s]

100%|██████████| 5/5 [00:00<00:00, 35.78it/s]

Parameter elasticities¶

+ =

In [7]:

elas = mc.parameter_elasticities(
    get_upper_glycolysis(),
    concs={
        "GLC": 0.3,
        "G6P": 0.4,
        "F6P": 0.5,
        "FBP": 0.6,
        "ATP": 0.4,
        "ADP": 0.6,
    },
    parameters=["k1", "k2", "k3"],
    mc_parameters=sample(
        {
            "k3": LogNormal(mean=np.log(0.25), sigma=1.0),
        },
        n=5,
    ),
)

_ = plot.violins_from_2d_idx(elas)
plt.show()

elas = mc.parameter_elasticities( get_upper_glycolysis(), concs={ "GLC": 0.3, "G6P": 0.4, "F6P": 0.5, "FBP": 0.6, "ATP": 0.4, "ADP": 0.6, }, parameters=["k1", "k2", "k3"], mc_parameters=sample( { "k3": LogNormal(mean=np.log(0.25), sigma=1.0), }, n=5, ), ) _ = plot.violins_from_2d_idx(elas) plt.show()

  0%|          | 0/5 [00:00<?, ?it/s]

100%|██████████| 5/5 [00:00<00:00, 35.73it/s]

Response coefficients¶

+ =

In [8]:

# Compare with "normal" control coefficients
rc = mca.response_coefficients(
    get_lin_chain_two_circles(),
    parameters=["vmax_1", "vmax_2", "vmax_3", "vmax_5", "vmax_6"],
)
_ = plot.heatmap(rc.concs)

mrc = mc.response_coefficients(
    get_lin_chain_two_circles(),
    parameters=["vmax_1", "vmax_2", "vmax_3", "vmax_5", "vmax_6"],
    mc_parameters=sample(
        {
            "k0": LogNormal(np.log(1.0), 1.0),
            "k4": LogNormal(np.log(0.5), 1.0),
        },
        n=10,
    ),
)

_ = plot.violins_from_2d_idx(mrc.concs, n_cols=len(mrc.concs.columns))

# Compare with "normal" control coefficients rc = mca.response_coefficients( get_lin_chain_two_circles(), parameters=["vmax_1", "vmax_2", "vmax_3", "vmax_5", "vmax_6"], ) _ = plot.heatmap(rc.concs) mrc = mc.response_coefficients( get_lin_chain_two_circles(), parameters=["vmax_1", "vmax_2", "vmax_3", "vmax_5", "vmax_6"], mc_parameters=sample( { "k0": LogNormal(np.log(1.0), 1.0), "k4": LogNormal(np.log(0.5), 1.0), }, n=10, ), ) _ = plot.violins_from_2d_idx(mrc.concs, n_cols=len(mrc.concs.columns))

  0%|          | 0/5 [00:00<?, ?it/s]

 20%|██        | 1/5 [00:00<00:01,  2.70it/s]

100%|██████████| 5/5 [00:00<00:00, 11.05it/s]

100%|██████████| 5/5 [00:00<00:00,  7.76it/s]

  0%|          | 0/10 [00:00<?, ?it/s]

  0%|          | 0/5 [00:00<?, ?it/s]

  0%|          | 0/5 [00:00<?, ?it/s]

  0%|          | 0/5 [00:00<?, ?it/s]

  0%|          | 0/5 [00:00<?, ?it/s]

 20%|██        | 1/5 [00:00<00:01,  3.25it/s]

 20%|██        | 1/5 [00:00<00:01,  2.25it/s]

 20%|██        | 1/5 [00:00<00:01,  2.05it/s]

 20%|██        | 1/5 [00:00<00:01,  2.07it/s]

 40%|████      | 2/5 [00:00<00:00,  3.17it/s]

 40%|████      | 2/5 [00:00<00:01,  2.35it/s]

 60%|██████    | 3/5 [00:00<00:00,  3.17it/s]

 40%|████      | 2/5 [00:00<00:01,  2.08it/s]

 40%|████      | 2/5 [00:00<00:01,  2.04it/s]

 80%|████████  | 4/5 [00:01<00:00,  3.18it/s]

 60%|██████    | 3/5 [00:01<00:00,  2.34it/s]

 60%|██████    | 3/5 [00:01<00:00,  2.09it/s]

 60%|██████    | 3/5 [00:01<00:00,  2.01it/s]

100%|██████████| 5/5 [00:01<00:00,  3.13it/s]

100%|██████████| 5/5 [00:01<00:00,  3.14it/s]

  0%|          | 0/5 [00:00<?, ?it/s]

 10%|█         | 1/10 [00:01<00:14,  1.64s/it]

 80%|████████  | 4/5 [00:01<00:00,  2.34it/s]

 80%|████████  | 4/5 [00:01<00:00,  2.09it/s]

 80%|████████  | 4/5 [00:01<00:00,  2.01it/s]

 20%|██        | 1/5 [00:00<00:01,  2.51it/s]

100%|██████████| 5/5 [00:02<00:00,  2.38it/s]

100%|██████████| 5/5 [00:02<00:00,  2.35it/s]

  0%|          | 0/5 [00:00<?, ?it/s]

100%|██████████| 5/5 [00:02<00:00,  2.10it/s]

100%|██████████| 5/5 [00:02<00:00,  2.09it/s]

  0%|          | 0/5 [00:00<?, ?it/s]

 40%|████      | 2/5 [00:00<00:01,  2.42it/s]

100%|██████████| 5/5 [00:02<00:00,  2.02it/s]

100%|██████████| 5/5 [00:02<00:00,  2.01it/s]

 20%|██        | 2/10 [00:02<00:09,  1.20s/it]

  0%|          | 0/5 [00:00<?, ?it/s]

 20%|██        | 1/5 [00:00<00:02,  1.56it/s]

 60%|██████    | 3/5 [00:01<00:00,  2.40it/s]

 20%|██        | 1/5 [00:00<00:01,  2.10it/s]

 20%|██        | 1/5 [00:00<00:01,  2.49it/s]

 80%|████████  | 4/5 [00:01<00:00,  2.46it/s]

 40%|████      | 2/5 [00:00<00:01,  2.52it/s]

 40%|████      | 2/5 [00:00<00:01,  2.04it/s]

 40%|████      | 2/5 [00:01<00:01,  1.53it/s]

100%|██████████| 5/5 [00:02<00:00,  2.43it/s]

100%|██████████| 5/5 [00:02<00:00,  2.43it/s]

 50%|█████     | 5/10 [00:03<00:03,  1.61it/s]

  0%|          | 0/5 [00:00<?, ?it/s]

 60%|██████    | 3/5 [00:01<00:00,  2.47it/s]

 60%|██████    | 3/5 [00:01<00:01,  1.99it/s]

 60%|██████    | 3/5 [00:01<00:01,  1.54it/s]

 80%|████████  | 4/5 [00:01<00:00,  2.45it/s]

 20%|██        | 1/5 [00:00<00:01,  2.18it/s]

 80%|████████  | 4/5 [00:01<00:00,  2.01it/s]

100%|██████████| 5/5 [00:02<00:00,  2.48it/s]

100%|██████████| 5/5 [00:02<00:00,  2.47it/s]

  0%|          | 0/5 [00:00<?, ?it/s]

 40%|████      | 2/5 [00:00<00:01,  2.16it/s]

 80%|████████  | 4/5 [00:02<00:00,  1.57it/s]

100%|██████████| 5/5 [00:02<00:00,  2.00it/s]

100%|██████████| 5/5 [00:02<00:00,  2.00it/s]

 20%|██        | 1/5 [00:00<00:01,  2.47it/s]

 60%|██████    | 3/5 [00:01<00:00,  2.17it/s]

100%|██████████| 5/5 [00:03<00:00,  1.70it/s]

100%|██████████| 5/5 [00:03<00:00,  1.63it/s]

 60%|██████    | 6/10 [00:05<00:03,  1.16it/s]

 40%|████      | 2/5 [00:00<00:01,  2.81it/s]

 80%|████████  | 4/5 [00:01<00:00,  2.44it/s]

 60%|██████    | 3/5 [00:00<00:00,  3.24it/s]

100%|██████████| 5/5 [00:01<00:00,  2.81it/s]

100%|██████████| 5/5 [00:01<00:00,  2.53it/s]

 90%|█████████ | 9/10 [00:05<00:00,  2.06it/s]

 80%|████████  | 4/5 [00:01<00:00,  3.54it/s]

100%|██████████| 5/5 [00:01<00:00,  3.78it/s]

100%|██████████| 5/5 [00:01<00:00,  3.43it/s]

100%|██████████| 10/10 [00:06<00:00,  2.19it/s]

100%|██████████| 10/10 [00:06<00:00,  1.65it/s]

First finish line

With that you now know most of what you will need from a day-to-day basis about monte carlo methods in modelbase2.

Congratulations!

Advanced topics¶

Parameter scans¶

Vary both monte carlo parameters as well as systematically scan for other parameters

In [9]:

mcss = mc.scan_steady_state(
    get_linear_chain_2v(),
    parameters=pd.DataFrame({"k1": np.linspace(0, 1, 3)}),
    mc_parameters=sample(
        {
            "k2": Uniform(1.0, 1.3),
            "k3": LogNormal(mean=1.0, sigma=0.2),
        },
        n=10,
    ),
)

plot.violins_from_2d_idx(mcss.concs)
plt.show()

mcss = mc.scan_steady_state( get_linear_chain_2v(), parameters=pd.DataFrame({"k1": np.linspace(0, 1, 3)}), mc_parameters=sample( { "k2": Uniform(1.0, 1.3), "k3": LogNormal(mean=1.0, sigma=0.2), }, n=10, ), ) plot.violins_from_2d_idx(mcss.concs) plt.show()

  0%|          | 0/10 [00:00<?, ?it/s]

  0%|          | 0/3 [00:00<?, ?it/s]

  0%|          | 0/3 [00:00<?, ?it/s]

  0%|          | 0/3 [00:00<?, ?it/s]

  0%|          | 0/3 [00:00<?, ?it/s]

100%|██████████| 3/3 [00:00<00:00, 26.35it/s]

100%|██████████| 3/3 [00:00<00:00, 24.91it/s]

100%|██████████| 3/3 [00:00<00:00, 26.27it/s]

100%|██████████| 3/3 [00:00<00:00, 25.42it/s]

 10%|█         | 1/10 [00:00<00:01,  6.09it/s]

100%|██████████| 3/3 [00:00<00:00, 25.53it/s]

100%|██████████| 3/3 [00:00<00:00, 23.10it/s]

100%|██████████| 3/3 [00:00<00:00, 26.69it/s]

100%|██████████| 3/3 [00:00<00:00, 25.01it/s]

  0%|          | 0/3 [00:00<?, ?it/s]

  0%|          | 0/3 [00:00<?, ?it/s]

  0%|          | 0/3 [00:00<?, ?it/s]

  0%|          | 0/3 [00:00<?, ?it/s]

100%|██████████| 3/3 [00:00<00:00, 31.27it/s]

  0%|          | 0/3 [00:00<?, ?it/s]

100%|██████████| 3/3 [00:00<00:00, 28.13it/s]

100%|██████████| 3/3 [00:00<00:00, 27.09it/s]

100%|██████████| 3/3 [00:00<00:00, 26.73it/s]

100%|██████████| 3/3 [00:00<00:00, 24.83it/s]

  0%|          | 0/3 [00:00<?, ?it/s]

100%|██████████| 3/3 [00:00<00:00, 29.10it/s]

100%|██████████| 3/3 [00:00<00:00, 24.66it/s]

 50%|█████     | 5/10 [00:00<00:00, 18.01it/s]

100%|██████████| 3/3 [00:00<00:00, 37.32it/s]

100%|██████████| 3/3 [00:00<00:00, 41.78it/s]

100%|██████████| 10/10 [00:00<00:00, 21.49it/s]

In [10]:

# FIXME: no idea how to plot this yet. Ridge plots?
# Maybe it's just a bit much :D

mcss = mc.scan_steady_state(
    get_linear_chain_2v(),
    parameters=mb2.cartesian_product(
        {
            "k1": np.linspace(0, 1, 3),
            "k2": np.linspace(0, 1, 3),
        }
    ),
    mc_parameters=sample(
        {
            "k3": LogNormal(mean=1.0, sigma=0.2),
        },
        n=10,
    ),
)

mcss.concs.head()

# FIXME: no idea how to plot this yet. Ridge plots? # Maybe it's just a bit much :D mcss = mc.scan_steady_state( get_linear_chain_2v(), parameters=mb2.cartesian_product( { "k1": np.linspace(0, 1, 3), "k2": np.linspace(0, 1, 3), } ), mc_parameters=sample( { "k3": LogNormal(mean=1.0, sigma=0.2), }, n=10, ), ) mcss.concs.head()

  0%|          | 0/10 [00:00<?, ?it/s]

  0%|          | 0/9 [00:00<?, ?it/s]

  0%|          | 0/9 [00:00<?, ?it/s]

  0%|          | 0/9 [00:00<?, ?it/s]

  0%|          | 0/9 [00:00<?, ?it/s]

 22%|██▏       | 2/9 [00:00<00:00, 19.15it/s]

 22%|██▏       | 2/9 [00:00<00:00, 17.04it/s]

 22%|██▏       | 2/9 [00:00<00:00, 15.91it/s]

 22%|██▏       | 2/9 [00:00<00:00, 14.93it/s]

 44%|████▍     | 4/9 [00:00<00:00, 19.44it/s]

 44%|████▍     | 4/9 [00:00<00:00, 17.68it/s]

 44%|████▍     | 4/9 [00:00<00:00, 16.01it/s]

 44%|████▍     | 4/9 [00:00<00:00, 15.43it/s]

 78%|███████▊  | 7/9 [00:00<00:00, 22.97it/s]

 78%|███████▊  | 7/9 [00:00<00:00, 22.05it/s]

 78%|███████▊  | 7/9 [00:00<00:00, 19.99it/s]

 78%|███████▊  | 7/9 [00:00<00:00, 19.11it/s]

100%|██████████| 9/9 [00:00<00:00, 23.34it/s]

  0%|          | 0/9 [00:00<?, ?it/s]

100%|██████████| 9/9 [00:00<00:00, 22.02it/s]

  0%|          | 0/9 [00:00<?, ?it/s]

100%|██████████| 9/9 [00:00<00:00, 20.37it/s]

  0%|          | 0/9 [00:00<?, ?it/s]

100%|██████████| 9/9 [00:00<00:00, 19.53it/s]

 10%|█         | 1/10 [00:00<00:04,  1.97it/s]

  0%|          | 0/9 [00:00<?, ?it/s]

 22%|██▏       | 2/9 [00:00<00:00, 19.86it/s]

 22%|██▏       | 2/9 [00:00<00:00, 15.75it/s]

 22%|██▏       | 2/9 [00:00<00:00, 18.58it/s]

 22%|██▏       | 2/9 [00:00<00:00, 18.64it/s]

 44%|████▍     | 4/9 [00:00<00:00, 19.30it/s]

 44%|████▍     | 4/9 [00:00<00:00, 16.67it/s]

 44%|████▍     | 4/9 [00:00<00:00, 17.64it/s]

 44%|████▍     | 4/9 [00:00<00:00, 18.29it/s]

 78%|███████▊  | 7/9 [00:00<00:00, 22.25it/s]

 67%|██████▋   | 6/9 [00:00<00:00, 18.00it/s]

100%|██████████| 9/9 [00:00<00:00, 23.27it/s]

 50%|█████     | 5/10 [00:00<00:00,  6.73it/s]

  0%|          | 0/9 [00:00<?, ?it/s]

 78%|███████▊  | 7/9 [00:00<00:00, 20.13it/s]

 78%|███████▊  | 7/9 [00:00<00:00, 21.29it/s]

100%|██████████| 9/9 [00:00<00:00, 21.12it/s]

100%|██████████| 9/9 [00:00<00:00, 21.77it/s]

  0%|          | 0/9 [00:00<?, ?it/s]

 89%|████████▉ | 8/9 [00:00<00:00, 17.58it/s]

 22%|██▏       | 2/9 [00:00<00:00, 19.17it/s]

100%|██████████| 9/9 [00:00<00:00, 18.22it/s]

 60%|██████    | 6/10 [00:00<00:00,  7.03it/s]

 33%|███▎      | 3/9 [00:00<00:00, 27.62it/s]

 67%|██████▋   | 6/9 [00:00<00:00, 30.20it/s]

100%|██████████| 9/9 [00:00<00:00, 32.60it/s]

 90%|█████████ | 9/10 [00:01<00:00, 10.11it/s]

 89%|████████▉ | 8/9 [00:00<00:00, 36.42it/s]

100%|██████████| 9/9 [00:00<00:00, 36.83it/s]

100%|██████████| 10/10 [00:01<00:00,  8.02it/s]

Out[10]:

			x	y
	k1	k2
0	0.0	0.0	1.000000e+00	-3.825562e-23
		0.5	-1.832836e-17	-2.579102e-18
		1.0	-7.161368e-17	-2.105052e-17
	0.5	0.0	NaN	NaN
		0.5	1.000000e+00	1.233791e-01

Custom distributions¶

If you want to create custom distributions, all you need to do is to create a class that follows the Distribution protocol, e.g. implements a sample function.

For API consistency, the sample method has to take rng argument, which can be ignored if not applicable.

In [11]:

from dataclasses import dataclass
from typing import TYPE_CHECKING

if TYPE_CHECKING:
    from modelbase2.types import Array


@dataclass
class MyOwnDistribution:
    loc: float = 0.0
    scale: float = 1.0

    def sample(
        self,
        num: int,
        rng: np.random.Generator | None = None,
    ) -> Array:
        if rng is None:
            rng = np.random.default_rng()
        return rng.normal(loc=self.loc, scale=self.scale, size=num)


sample({"p1": MyOwnDistribution()}, n=5)

from dataclasses import dataclass from typing import TYPE_CHECKING if TYPE_CHECKING: from modelbase2.types import Array @dataclass class MyOwnDistribution: loc: float = 0.0 scale: float = 1.0 def sample( self, num: int, rng: np.random.Generator | None = None, ) -> Array: if rng is None: rng = np.random.default_rng() return rng.normal(loc=self.loc, scale=self.scale, size=num) sample({"p1": MyOwnDistribution()}, n=5)

Out[11]:

	p1
0	-2.450373
1	-1.319903
2	2.309143
3	1.055451
4	0.093289

In [ ]: