Label models

In [1]:

from __future__ import annotations

from typing import Any

import matplotlib.pyplot as plt

from example_models import get_linear_chain_2v, get_tpi_ald_model
from modelbase2 import (
    LabelMapper,
    LinearLabelMapper,
    Simulator,
    plot,
)
from modelbase2.types import unwrap, unwrap2


def print_annotated(description: str, value: Any) -> None:
    print(
        description,
        value,
        sep="\n",
        end="\n\n",
    )

from __future__ import annotations from typing import Any import matplotlib.pyplot as plt from example_models import get_linear_chain_2v, get_tpi_ald_model from modelbase2 import ( LabelMapper, LinearLabelMapper, Simulator, plot, ) from modelbase2.types import unwrap, unwrap2 def print_annotated(description: str, value: Any) -> None: print( description, value, sep="\n", end="\n\n", )

Labeled models¶

Labelled models allow explicitly mapping the transitions between isotopomers variables.
This, for example, allows building models of the Calvin-Benson-Bassham cycle, in which each carbon atom can be labelled individually:

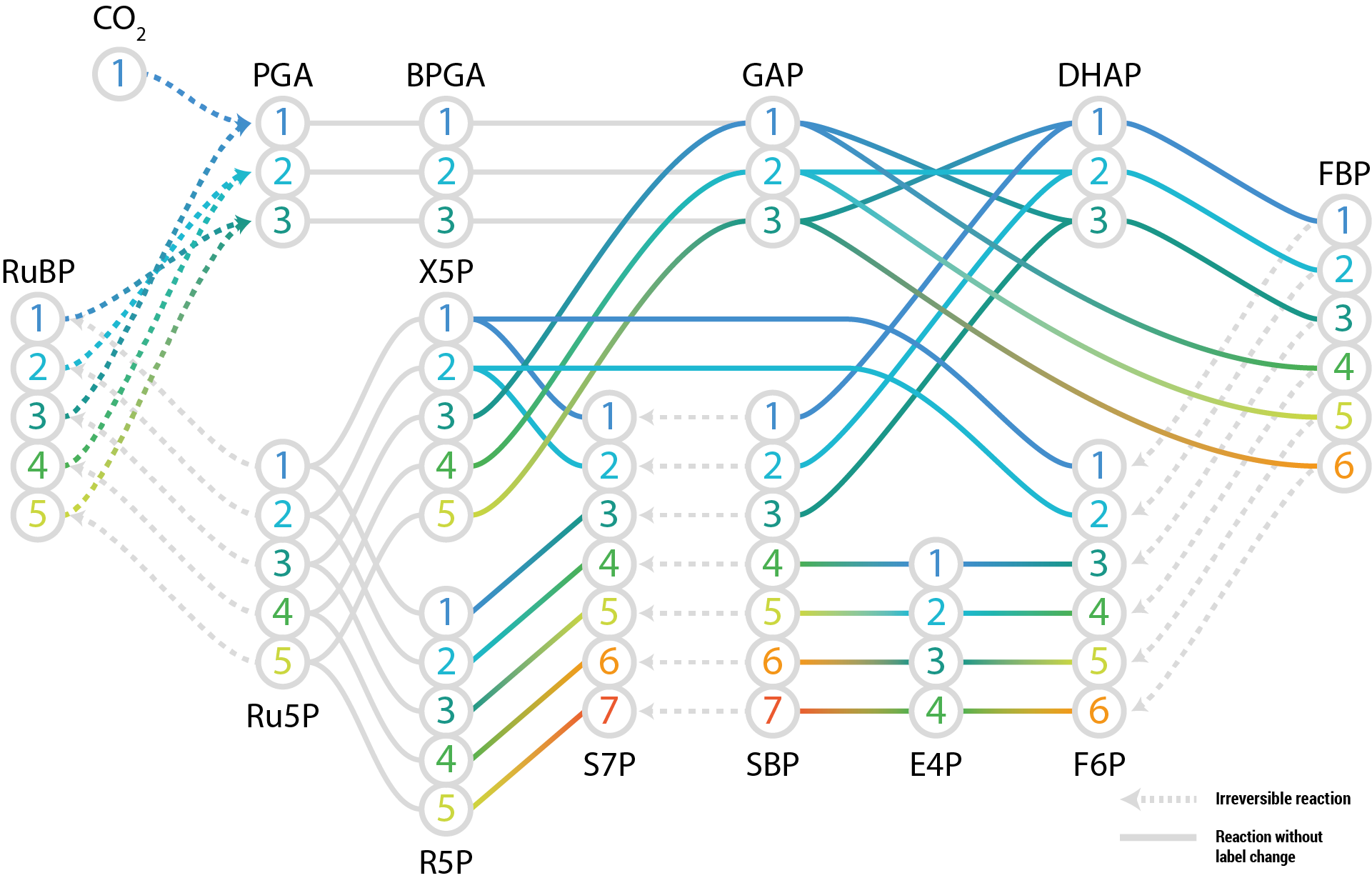
modelbase includes a LabelMapper that takes

• a model
• a dictionary mapping the variables to the amount of label positions they have
• a transition map

to auto-generate all possible 2^n variants of the variables and reaction transitions between them.

As an example let's take triose phosphate isomerase, which catalyzes the interconversion of glyceraldehyde 3-phosphate (GAP) and dihydroxyacetone phosphate (DHAP).
As illustrated below, in the case of the forward reaction the first and last carbon atoms are swapped

So DHAP(1) is build from GAP(3), DHAP(2) from GAP(2) and DHAP(3) from GAP(1).
We notate this using normal 0-based indexing as follows

label_maps = {"TPIf": [2, 1, 0]}

In [2]:

mapper = LabelMapper(
    get_tpi_ald_model(),
    label_variables={"GAP": 3, "DHAP": 3, "FBP": 6},
    label_maps={
        "TPIf": [2, 1, 0],
        "TPIr": [2, 1, 0],
        "ALDf": [0, 1, 2, 3, 4, 5],
        "ALDr": [0, 1, 2, 3, 4, 5],
    },
)


labels = unwrap(
    Simulator(mapper.build_model(initial_labels={"GAP": 0}))
    .simulate(20)
    .get_full_concs()
)

fig, ax = plot.relative_label_distribution(mapper, labels, n_cols=3)
plt.show()

mapper = LabelMapper( get_tpi_ald_model(), label_variables={"GAP": 3, "DHAP": 3, "FBP": 6}, label_maps={ "TPIf": [2, 1, 0], "TPIr": [2, 1, 0], "ALDf": [0, 1, 2, 3, 4, 5], "ALDr": [0, 1, 2, 3, 4, 5], }, ) labels = unwrap( Simulator(mapper.build_model(initial_labels={"GAP": 0})) .simulate(20) .get_full_concs() ) fig, ax = plot.relative_label_distribution(mapper, labels, n_cols=3) plt.show()

Linear label mapper¶

The LabelMapper makes no assumptions about the state of the model, which causes a lot of complexity.
In steady-state however, the space of possible solutions is reduced and the labelling dynamics can be represented by a set of linear differential equations.
See Sokol and Portais 2015 for the theory of dynamic label propagation under the stationary assumption.

In [3]:

model_fn = get_tpi_ald_model()

concs, fluxes = unwrap2(Simulator(model_fn).simulate(20).get_concs_and_fluxes())


mapper = LinearLabelMapper(
    model_fn,
    label_variables={"GAP": 3, "DHAP": 3, "FBP": 6},
    label_maps={
        "TPIf": [2, 1, 0],
        "TPIr": [2, 1, 0],
        "ALDf": [0, 1, 2, 3, 4, 5],
        "ALDr": [0, 1, 2, 3, 4, 5],
    },
)


labels = unwrap(
    Simulator(
        mapper.build_model(
            concs=concs.iloc[-1],
            fluxes=fluxes.iloc[-1],
            initial_labels={"GAP": 0},
        )
    )
    .simulate(20)
    .get_full_concs()
)
fig, ax = plot.relative_label_distribution(mapper, labels, n_cols=3)
plt.show()

model_fn = get_tpi_ald_model() concs, fluxes = unwrap2(Simulator(model_fn).simulate(20).get_concs_and_fluxes()) mapper = LinearLabelMapper( model_fn, label_variables={"GAP": 3, "DHAP": 3, "FBP": 6}, label_maps={ "TPIf": [2, 1, 0], "TPIr": [2, 1, 0], "ALDf": [0, 1, 2, 3, 4, 5], "ALDr": [0, 1, 2, 3, 4, 5], }, ) labels = unwrap( Simulator( mapper.build_model( concs=concs.iloc[-1], fluxes=fluxes.iloc[-1], initial_labels={"GAP": 0}, ) ) .simulate(20) .get_full_concs() ) fig, ax = plot.relative_label_distribution(mapper, labels, n_cols=3) plt.show()

First finish line

With that you now know most of what you will need from a day-to-day basis about labelled models in modelbase2.

Congratulations!

Advanced topics¶

External & initial labels¶

In the case of open models, we make the assumption that there is a static pool of external labels.
For example, this could be the labelled portion of ambient carbon dioxide.
We denote that external label pool with EXT and by default set the value 1.0 to it, which means that it is fully labelled.

In [4]:

model = get_linear_chain_2v()
concs, fluxes = unwrap2(Simulator(model).simulate(100).get_concs_and_fluxes())
mapper = LinearLabelMapper(
    model,
    label_variables={"x": 2, "y": 2},
    label_maps={
        "v1": [0, 1],
        "v2": [0, 1],
        "v3": [0, 1],
    },
)

label_model = mapper.build_model(
    concs=concs.iloc[-1],
    fluxes=fluxes.iloc[-1],
)

# Access the external label pool
print(label_model.parameters["EXT"])

# A reaction that consumes the external label pool
print(label_model.reactions["v1__0"].args)

# A reaction that doesn't require the external label pool
print(label_model.reactions["v2__0"].args)

model = get_linear_chain_2v() concs, fluxes = unwrap2(Simulator(model).simulate(100).get_concs_and_fluxes()) mapper = LinearLabelMapper( model, label_variables={"x": 2, "y": 2}, label_maps={ "v1": [0, 1], "v2": [0, 1], "v3": [0, 1], }, ) label_model = mapper.build_model( concs=concs.iloc[-1], fluxes=fluxes.iloc[-1], ) # Access the external label pool print(label_model.parameters["EXT"]) # A reaction that consumes the external label pool print(label_model.reactions["v1__0"].args) # A reaction that doesn't require the external label pool print(label_model.reactions["v2__0"].args)

1.0
['EXT', 'v1']
['x__0', 'v2']

You can modify the external concentration to your liking by simply updating the parameter value.

In [5]:

fig, ax = plot.relative_label_distribution(
    mapper,
    unwrap(
        Simulator(label_model)
        .update_parameter("EXT", 1.0)  # update exeternal label to fully labelled
        .simulate(20)
        .get_full_concs()
    ),
    n_cols=3,
)
fig.suptitle("Fully labelled external pool")
plt.show()

fig, ax = plot.relative_label_distribution( mapper, unwrap( Simulator(label_model) .update_parameter("EXT", 1.0) # update exeternal label to fully labelled .simulate(20) .get_full_concs() ), n_cols=3, ) fig.suptitle("Fully labelled external pool") plt.show()

In [6]:

fig, axs = plot.relative_label_distribution(
    mapper,
    unwrap(
        Simulator(label_model)
        .update_parameter("EXT", 0.5)  # update external label to half labelled
        .simulate(20)
        .get_full_concs()
    ),
    n_cols=3,
)
fig.suptitle("Half labelled external pool")
for ax in axs:
    ax.set_ylim(0, 1)
plt.show()

fig, axs = plot.relative_label_distribution( mapper, unwrap( Simulator(label_model) .update_parameter("EXT", 0.5) # update external label to half labelled .simulate(20) .get_full_concs() ), n_cols=3, ) fig.suptitle("Half labelled external pool") for ax in axs: ax.set_ylim(0, 1) plt.show()

Somewhat trivially, if you have no external label, there is no influx of labels

In [7]:

fig, axs = plot.relative_label_distribution(
    mapper,
    unwrap(
        Simulator(label_model)
        .update_parameter("EXT", 0.0)
        .simulate(20)
        .get_full_concs()
    ),
    n_cols=3,
)
fig.suptitle("No labelled external pool")
for ax in axs:
    ax.set_ylim(0, 1)
plt.show()

fig, axs = plot.relative_label_distribution( mapper, unwrap( Simulator(label_model) .update_parameter("EXT", 0.0) .simulate(20) .get_full_concs() ), n_cols=3, ) fig.suptitle("No labelled external pool") for ax in axs: ax.set_ylim(0, 1) plt.show()

However, we can imagine a scenario where some initial labels are given, even though there is no external labeling.
You can achieve that by updating the initial conditions like so.

In [8]:

fig, axs = plot.relative_label_distribution(
    mapper,
    unwrap(
        Simulator(label_model, y0=label_model.get_initial_conditions() | {"x__0": 1.0})
        .update_parameter("EXT", 0.0)
        .simulate(20)
        .get_full_concs()
    ),
    n_cols=3,
)
fig.suptitle("No labelled external pool")
for ax in axs:
    ax.set_ylim(0, 1)
plt.show()

fig, axs = plot.relative_label_distribution( mapper, unwrap( Simulator(label_model, y0=label_model.get_initial_conditions() | {"x__0": 1.0}) .update_parameter("EXT", 0.0) .simulate(20) .get_full_concs() ), n_cols=3, ) fig.suptitle("No labelled external pool") for ax in axs: ax.set_ylim(0, 1) plt.show()

For convenience, the build_model function also allows you to set the external labels and the initial labels.
Here, initial_labels specifies the position at which the initial label is given.

In [9]:

label_model = mapper.build_model(
    concs=concs.iloc[-1],
    fluxes=fluxes.iloc[-1],
    external_label=0.0,
    initial_labels={"x": 0},
)

fig, axs = plot.relative_label_distribution(
    mapper, unwrap(Simulator(label_model).simulate(20).get_full_concs()), n_cols=3
)
fig.suptitle("No external label, but initial label in C1 of x")
plt.show()

label_model = mapper.build_model( concs=concs.iloc[-1], fluxes=fluxes.iloc[-1], external_label=0.0, initial_labels={"x": 0}, ) fig, axs = plot.relative_label_distribution( mapper, unwrap(Simulator(label_model).simulate(20).get_full_concs()), n_cols=3 ) fig.suptitle("No external label, but initial label in C1 of x") plt.show()

You can also distribute that initial label across multiple label positions of the variable.

In [10]:

label_model = mapper.build_model(
    concs=concs.iloc[-1],
    fluxes=fluxes.iloc[-1],
    external_label=0.0,
    initial_labels={"x": [0, 1]},
)

fig, axs = plot.relative_label_distribution(
    mapper, unwrap(Simulator(label_model).simulate(20).get_full_concs()), n_cols=3
)
fig.suptitle("No external label, but initial label in C1 & C2 of x")
plt.show()

label_model = mapper.build_model( concs=concs.iloc[-1], fluxes=fluxes.iloc[-1], external_label=0.0, initial_labels={"x": [0, 1]}, ) fig, axs = plot.relative_label_distribution( mapper, unwrap(Simulator(label_model).simulate(20).get_full_concs()), n_cols=3 ) fig.suptitle("No external label, but initial label in C1 & C2 of x") plt.show()