In [1]:

from __future__ import annotations

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

import modelbase2 as mb2
from example_models import (
    get_linear_chain_2v,
)
from modelbase2 import make_protocol, plot, scan

from __future__ import annotations import matplotlib.pyplot as plt import numpy as np import pandas as pd import modelbase2 as mb2 from example_models import ( get_linear_chain_2v, ) from modelbase2 import make_protocol, plot, scan

Parameter scans¶

Parameter scans allow you to systematically assess the behaviour of your model dependent on the value of one or more parameters.
modelbase2 has routines to scan over, and easily visualise time courses, protocol time courses, and steady states for one or more parameters.

For this, we import the scan and plot modules from which contain the respective routines.

Steady-state¶

The steady-state scan takes a pandas.DataFrame of parameters to be scanned as an input and returns the steady-states at the respective parameter values.

The DataFrame can take an arbitrary number of parameters and should be in the following format

n	k1
0	1
1	1.2
2	1.4

As an example we will use a linear chain of two reactions like this

$$ \varnothing \xrightarrow{v_1} S \xrightarrow{v_2} P \xrightarrow{v_3} \varnothing$$

In [2]:

res = scan.steady_state(
    get_linear_chain_2v(),
    parameters=pd.DataFrame({"k1": np.linspace(1, 3, 11)}),
)

fig, (ax1, ax2) = plot.two_axes(figsize=(7, 3))
plot.lines(res.concs, ax=ax1)  # access concentrations by name
plot.lines(res.fluxes, ax=ax2)  # access fluxes by name

ax1.set(ylabel="Concentration / a.u.")
ax2.set(ylabel="Flux / a.u.")
plt.show()

res = scan.steady_state( get_linear_chain_2v(), parameters=pd.DataFrame({"k1": np.linspace(1, 3, 11)}), ) fig, (ax1, ax2) = plot.two_axes(figsize=(7, 3)) plot.lines(res.concs, ax=ax1) # access concentrations by name plot.lines(res.fluxes, ax=ax2) # access fluxes by name ax1.set(ylabel="Concentration / a.u.") ax2.set(ylabel="Flux / a.u.") plt.show()

  0%|          | 0/11 [00:00<?, ?it/s]

 82%|████████▏ | 9/11 [00:00<00:00, 74.29it/s]

100%|██████████| 11/11 [00:00<00:00, 69.56it/s]

All scans return a result object, which allow multiple access patterns for convenience.

Namely, the concentrations and fluxes can be accessed by name, unpacked or combined into a single dataframe.

In [3]:

# Access by name
_ = res.concs
_ = res.fluxes

# scan can be unpacked
concs, fluxes = res

# combine concs and fluxes as single dataframe
_ = res.results

# Access by name _ = res.concs _ = res.fluxes # scan can be unpacked concs, fluxes = res # combine concs and fluxes as single dataframe _ = res.results

Combinations¶

Often you want to scan over multiple parameters at the same time.
The recommended way to do this is to use the cartesian_product function, which takes a parameter_name: values mapping and creates a pandas.DataFrame of their combinations from it (think nested for loop).

In the case the parameters DataFrame contains more than one column, the returned pandas.DataFrame will contain a pandas.MultiIndex.

In [4]:

mb2.cartesian_product(
    {
        "k1": [1, 2],
        "k2": [3, 4],
    }
)

mb2.cartesian_product( { "k1": [1, 2], "k2": [3, 4], } )

Out[4]:

	k1	k2
0	1	3
1	1	4
2	2	3
3	2	4

In [5]:

res = scan.steady_state(
    get_linear_chain_2v(),
    parameters=mb2.cartesian_product(
        {
            "k1": np.linspace(1, 2, 3),
            "k2": np.linspace(1, 2, 4),
        }
    ),
)

res.results.head()

res = scan.steady_state( get_linear_chain_2v(), parameters=mb2.cartesian_product( { "k1": np.linspace(1, 2, 3), "k2": np.linspace(1, 2, 4), } ), ) res.results.head()

  0%|          | 0/12 [00:00<?, ?it/s]

 83%|████████▎ | 10/12 [00:00<00:00, 87.51it/s]

100%|██████████| 12/12 [00:00<00:00, 83.62it/s]

Out[5]:

		x	y	v1	v2	v3
k1	k2
1.0	1.000000	1.00	1.0	1.0	1.0	1.0
	1.333333	0.75	1.0	1.0	1.0	1.0
	1.666667	0.60	1.0	1.0	1.0	1.0
	2.000000	0.50	1.0	1.0	1.0	1.0
1.5	1.000000	1.50	1.5	1.5	1.5	1.5

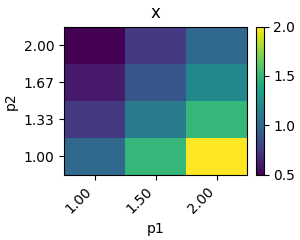
You can plot the results of a single variable of this scan using a heatmap

In [6]:

plot.heatmap_from_2d_idx(res.concs, variable="x")
plt.show()

plot.heatmap_from_2d_idx(res.concs, variable="x") plt.show()

Or create heatmaps of all passed variables at once.

In [7]:

plot.heatmaps_from_2d_idx(res.concs)
plt.show()

plot.heatmaps_from_2d_idx(res.concs) plt.show()

You can also combine more than two parameters, however, visualisation then becomes challenging.

In [8]:

res = scan.steady_state(
    get_linear_chain_2v(),
    mb2.cartesian_product(
        {
            "k1": np.linspace(1, 2, 3),
            "k2": np.linspace(1, 2, 4),
            "k3": np.linspace(1, 2, 4),
        }
    ),
)
res.results.head()

res = scan.steady_state( get_linear_chain_2v(), mb2.cartesian_product( { "k1": np.linspace(1, 2, 3), "k2": np.linspace(1, 2, 4), "k3": np.linspace(1, 2, 4), } ), ) res.results.head()

  0%|          | 0/48 [00:00<?, ?it/s]

 19%|█▉        | 9/48 [00:00<00:00, 88.95it/s]

 52%|█████▏    | 25/48 [00:00<00:00, 127.63it/s]

 88%|████████▊ | 42/48 [00:00<00:00, 137.75it/s]

100%|██████████| 48/48 [00:00<00:00, 103.77it/s]

Out[8]:

			x	y	v1	v2	v3
k1	k2	k3
1.0	1.000000	1.000000	1.00	1.00	1.0	1.0	1.0
		1.333333	1.00	0.75	1.0	1.0	1.0
		1.666667	1.00	0.60	1.0	1.0	1.0
		2.000000	1.00	0.50	1.0	1.0	1.0
	1.333333	1.000000	0.75	1.00	1.0	1.0	1.0

Time course¶

You can perform a time course for each of the parameter values, resulting in a distribution of time courses.
The index now also contains the time, so even for one parameter a pandas.MultiIndex is used.

In [9]:

tss = scan.time_course(
    get_linear_chain_2v(),
    parameters=pd.DataFrame({"k1": np.linspace(1, 2, 11)}),
    time_points=np.linspace(0, 1, 11),
)

fig, (ax1, ax2) = plot.two_axes(figsize=(7, 4))
plot.lines_mean_std_from_2d_idx(tss.concs, ax=ax1)
plot.lines_mean_std_from_2d_idx(tss.fluxes, ax=ax2)

ax1.set(xlabel="time / a.u.", ylabel="Concentration / a.u.")
ax2.set(xlabel="time / a.u.", ylabel="Flux / a.u.")
plt.show()

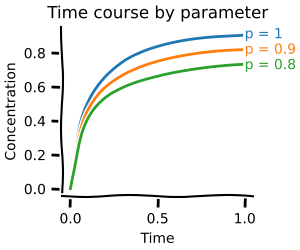
tss = scan.time_course( get_linear_chain_2v(), parameters=pd.DataFrame({"k1": np.linspace(1, 2, 11)}), time_points=np.linspace(0, 1, 11), ) fig, (ax1, ax2) = plot.two_axes(figsize=(7, 4)) plot.lines_mean_std_from_2d_idx(tss.concs, ax=ax1) plot.lines_mean_std_from_2d_idx(tss.fluxes, ax=ax2) ax1.set(xlabel="time / a.u.", ylabel="Concentration / a.u.") ax2.set(xlabel="time / a.u.", ylabel="Flux / a.u.") plt.show()

  0%|          | 0/11 [00:00<?, ?it/s]

100%|██████████| 11/11 [00:00<00:00, 79.95it/s]

Again, this works for an arbitray number of parameters.

In [10]:

tss = scan.time_course(
    get_linear_chain_2v(),
    parameters=mb2.cartesian_product(
        {
            "k1": np.linspace(1, 2, 11),
            "k2": np.linspace(1, 2, 4),
        }
    ),
    time_points=np.linspace(0, 1, 11),
)


fig, (ax1, ax2) = plot.two_axes(figsize=(7, 4))
plot.lines_mean_std_from_2d_idx(tss.concs, ax=ax1)
plot.lines_mean_std_from_2d_idx(tss.fluxes, ax=ax2)
ax1.set(xlabel="time / a.u.", ylabel="Concentration / a.u.")
ax2.set(xlabel="time / a.u.", ylabel="Flux / a.u.")
plt.show()

tss = scan.time_course( get_linear_chain_2v(), parameters=mb2.cartesian_product( { "k1": np.linspace(1, 2, 11), "k2": np.linspace(1, 2, 4), } ), time_points=np.linspace(0, 1, 11), ) fig, (ax1, ax2) = plot.two_axes(figsize=(7, 4)) plot.lines_mean_std_from_2d_idx(tss.concs, ax=ax1) plot.lines_mean_std_from_2d_idx(tss.fluxes, ax=ax2) ax1.set(xlabel="time / a.u.", ylabel="Concentration / a.u.") ax2.set(xlabel="time / a.u.", ylabel="Flux / a.u.") plt.show()

  0%|          | 0/44 [00:00<?, ?it/s]

 32%|███▏      | 14/44 [00:00<00:00, 136.42it/s]

100%|██████████| 44/44 [00:00<00:00, 180.13it/s]

The scan object returned has a pandas.MultiIndex of n x time, where n is an index that references parameter combinations.
You can access the referenced parameters using .parameters

In [11]:

tss.parameters.head()

tss.parameters.head()

Out[11]:

	k1	k2
0	1.0	1.000000
1	1.0	1.333333
2	1.0	1.666667
3	1.0	2.000000
4	1.1	1.000000

You can also easily access common aggregates like mean and standard deviation (std) using get_agg_per_time.

In [12]:

tss.get_agg_per_time("std").head()

tss.get_agg_per_time("std").head()

Out[12]:

	x	y	v1	v2	v3
time
0.0	0.000000	0.000000	0.319884	0.376987	0.000000
0.1	0.045932	0.033365	0.319884	0.328164	0.033365
0.2	0.085571	0.059438	0.319884	0.293370	0.059438
0.3	0.119871	0.079991	0.319884	0.270384	0.079991
0.4	0.149628	0.096455	0.319884	0.256845	0.096455

Protocol¶

The same can be done for protocols.

In [13]:

res = scan.time_course_over_protocol(
    get_linear_chain_2v(),
    parameters=pd.DataFrame({"k2": np.linspace(1, 2, 11)}),
    protocol=make_protocol(
        [
            (1, {"k1": 1}),
            (2, {"k1": 2}),
            (3, {"k1": 1}),
        ]
    ),
)

fig, (ax1, ax2) = plot.two_axes(figsize=(7, 4))
plot.lines_mean_std_from_2d_idx(res.concs, ax=ax1)
plot.lines_mean_std_from_2d_idx(res.fluxes, ax=ax2)
ax1.set(xlabel="time / a.u.", ylabel="Concentration / a.u.")
ax2.set(xlabel="time / a.u.", ylabel="Flux / a.u.")

for ax in (ax1, ax2):
    plot.shade_protocol(res.protocol["k1"], ax=ax, alpha=0.2)
plt.show()

res = scan.time_course_over_protocol( get_linear_chain_2v(), parameters=pd.DataFrame({"k2": np.linspace(1, 2, 11)}), protocol=make_protocol( [ (1, {"k1": 1}), (2, {"k1": 2}), (3, {"k1": 1}), ] ), ) fig, (ax1, ax2) = plot.two_axes(figsize=(7, 4)) plot.lines_mean_std_from_2d_idx(res.concs, ax=ax1) plot.lines_mean_std_from_2d_idx(res.fluxes, ax=ax2) ax1.set(xlabel="time / a.u.", ylabel="Concentration / a.u.") ax2.set(xlabel="time / a.u.", ylabel="Flux / a.u.") for ax in (ax1, ax2): plot.shade_protocol(res.protocol["k1"], ax=ax, alpha=0.2) plt.show()

  0%|          | 0/11 [00:00<?, ?it/s]

 45%|████▌     | 5/11 [00:00<00:00, 43.22it/s]

100%|██████████| 11/11 [00:00<00:00, 45.57it/s]

First finish line

With that you now know most of what you will need from a day-to-day basis about parameter scans in modelbase2.

Congratulations!

In [14]:

import pickle
from pathlib import Path
from typing import TYPE_CHECKING, Any

from modelbase2.parallel import Cache, parallelise

if TYPE_CHECKING:
    from collections.abc import Hashable

import pickle from pathlib import Path from typing import TYPE_CHECKING, Any from modelbase2.parallel import Cache, parallelise if TYPE_CHECKING: from collections.abc import Hashable

Parallel execution¶

By default, all scans are executed in parallel.
To do this, they internally use the parallelise function defined by modelbase.

Tip: You can also use this function for other analyses as it is not specific to any modelbase constructs.

The parallelise takes a function of type T and an iterable of a key: T pair.
The key is used to construct a dictionary of results and for caching (see below).

In [15]:

def square(x: float) -> float:
    return x**2


output = parallelise(square, [("a", 2), ("b", 3), ("c", 4)])
output

def square(x: float) -> float: return x**2 output = parallelise(square, [("a", 2), ("b", 3), ("c", 4)]) output

  0%|          | 0/3 [00:00<?, ?it/s]

100%|██████████| 3/3 [00:00<00:00, 19.10it/s]

Out[15]:

{'a': 4, 'b': 9, 'c': 16}

Caching¶

In case the simulations take a significant amount of time to run, it makes sense to cache the results on disk.
You can do that by adding a cache to the parallelise function (and thus to all scan functions as well).

parallelise(...,  cache=Cache())

The first time the scan is run, the calculations are done, every subsequent time the results are loaded.

In [16]:

output = parallelise(
    square,
    [("a", 2), ("b", 3), ("c", 4)],
    cache=Cache(),
)

output = parallelise( square, [("a", 2), ("b", 3), ("c", 4)], cache=Cache(), )

  0%|          | 0/3 [00:00<?, ?it/s]

100%|██████████| 3/3 [00:00<00:00, 22.12it/s]

To avoid overwriting cache results by different analyses we recommend saving each of them in a respective folder.

In [17]:

_ = Cache(tmp_dir=Path(".cache") / "analysis-name")

_ = Cache(tmp_dir=Path(".cache") / "analysis-name")

By default the key of parallelise is used to create a pickle file called {k}.p.
You can customise this behaviour by changing the name_fn, load_fn and save_fn arguments respectively.

In [18]:

def _pickle_name(k: Hashable) -> str:
    return f"{k}.p"


def _pickle_load(file: Path) -> Any:
    with file.open("rb") as fp:
        return pickle.load(fp)


def _pickle_save(file: Path, data: Any) -> None:
    with file.open("wb") as fp:
        pickle.dump(data, fp)


_ = Cache(
    name_fn=_pickle_name,
    load_fn=_pickle_load,
    save_fn=_pickle_save,
)

def _pickle_name(k: Hashable) -> str: return f"{k}.p" def _pickle_load(file: Path) -> Any: with file.open("rb") as fp: return pickle.load(fp) def _pickle_save(file: Path, data: Any) -> None: with file.open("wb") as fp: pickle.dump(data, fp) _ = Cache( name_fn=_pickle_name, load_fn=_pickle_load, save_fn=_pickle_save, )