Fitting
from __future__ import annotations
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import minimize
from example_models import get_linear_chain_2v
from modelbase2 import Simulator, fit, plot
from modelbase2.types import unwrap
Fitting¶
Almost every model at some point needs to be fitted to experimental data to be validated.
modelbase2 offers highly customisable routines for fitting either time series or steady-states.
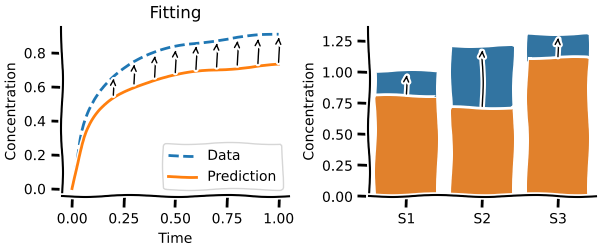
For this tutorial we are going to use the fit module to optimise our parameter values and the plot module to plot some results.
Let's get started!
Creating synthetic data¶
Normally, you would fit your model to experimental data.
Here, for the sake of simplicity, we will generate some synthetic data.
Checkout the basics tutorial if you need a refresher on building and simulating models.
# As a small trick, let's define a variable for the model function
# That way, we can re-use it all over the file and easily replace
# it with another model
model_fn = get_linear_chain_2v
res = unwrap(
Simulator(model_fn())
.update_parameters({"k1": 1.0, "k2": 2.0, "k3": 1.0})
.simulate_time_course(np.linspace(0, 10, 101))
.get_result()
).get_combined()
fig, ax = plot.lines(res)
ax.set(xlabel="time / a.u.", ylabel="Conc. & Flux / a.u.")
plt.show()
Steady-states¶
For the steady-state fit we need two inputs:
- the steady state data, which we supply as a
pandas.Series - an initial parameter guess
The fitting routine will compare all data contained in that series to the model output.
Note that the data both contains concentrations and fluxes!
data = res.iloc[-1]
data.head()
x 0.500000 y 1.000045 v1 1.000000 v2 1.000000 v3 1.000045 Name: 10.0, dtype: float64
fit.steady_state(
model_fn(),
p0={"k1": 1.038, "k2": 1.87, "k3": 1.093},
data=res.iloc[-1],
)
{'k1': np.float64(1.0000152020440245),
'k2': np.float64(2.0000309241277257),
'k3': np.float64(0.9999697811318708)}
If only some of the data is required, you can use a subset of it.
The fitting routine will only try to fit concentrations and fluxes contained in that series.
fit.steady_state(
model_fn(),
p0={"k1": 1.038, "k2": 1.87, "k3": 1.093},
data=data.loc[["x", "y"]],
)
{'k1': np.float64(0.9829433879975833),
'k2': np.float64(1.9658867514111864),
'k3': np.float64(0.9828987685876319)}
Time course¶
For the time course fit we need again need two inputs
- the time course data, which we supply as a
pandas.DataFrame - an initial parameter guess
The fitting routine will create data at every time points specified in the DataFrame and compare all of them.
Other than that, the same rules of the steady-state fitting apply.
fit.time_course(
model_fn(),
p0={"k1": 1.038, "k2": 1.87, "k3": 1.093},
data=res,
)
{'k1': np.float64(0.9999999948105439),
'k2': np.float64(1.9999999615790365),
'k3': np.float64(0.999999992228362)}
First finish line
With that you now know most of what you will need from a day-to-day basis about fitting in modelbase2.Congratulations!
Advanced topics / customisation¶
You can use dependency injection to overwrite the minimisation function as well as the residual function and the integrator.
Here we create a custom minimization function.
from typing import TYPE_CHECKING
if TYPE_CHECKING:
from modelbase2.fit import ResidualFn
def nelder_mead(
residual_fn: ResidualFn,
p0: dict[str, float],
) -> dict[str, float]:
res = minimize(
residual_fn,
x0=list(p0.values()),
method="Nelder-Mead",
)
if res.success:
return dict(
zip(
p0,
res.x,
strict=True,
)
)
return dict(zip(p0, np.full(len(p0), np.nan, dtype=float), strict=True))
fit.time_course(
model_fn(),
p0={"k1": 1.038, "k2": 1.87, "k3": 1.093},
data=res,
minimize_fn=nelder_mead,
)
{'k1': np.float64(1.0000044128393781),
'k2': np.float64(1.9999586259064912),
'k3': np.float64(1.000005095705572)}